题目内容
已知数列{an}中,a1=1,a2=a-1(a≠0且a≠1),其前n项和为Sn,且当n≥2时,S2n=Sn-1Sn+1。
(1)求数列{an}的通项公式;
(Ⅱ)若a=4,令 ,记数列{bn}的前n项和为Tn,设λ是整数,问是否存在正整数n,使等式
,记数列{bn}的前n项和为Tn,设λ是整数,问是否存在正整数n,使等式 成立?若存在,求出n和相应的λ 值;若不存在,请说明理由。
成立?若存在,求出n和相应的λ 值;若不存在,请说明理由。
(1)求数列{an}的通项公式;
(Ⅱ)若a=4,令
 ,记数列{bn}的前n项和为Tn,设λ是整数,问是否存在正整数n,使等式
,记数列{bn}的前n项和为Tn,设λ是整数,问是否存在正整数n,使等式 成立?若存在,求出n和相应的λ 值;若不存在,请说明理由。
成立?若存在,求出n和相应的λ 值;若不存在,请说明理由。解:(1)∵n≥2时,
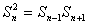
∴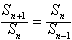
又S1=1≠0,S2=a1+a2=a≠0,
∴{Sn}是首项为1,公比q=a的等比数列
∴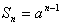
当n≥2时,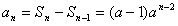
又a1=S1=1
∴ 。
。
(2)当a=4,n≥2时
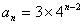
此时
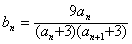
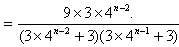
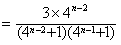
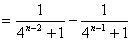 }
}
又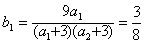
∴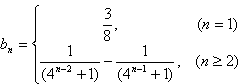
故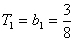
当n≥2时,Tn=b1+b2+…+bn
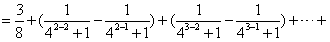
=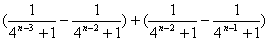
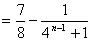
若n=1,则等式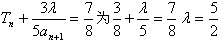 不是整数,不符合题意;
不是整数,不符合题意;
若n≥2,则等式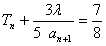 为
为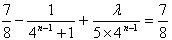
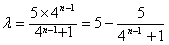
∵λ是整数,
∴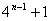 必是5的因数
必是5的因数
∵n≥2时, ∴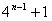 ≥5
≥5
当且仅当n=2时,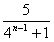 是整数,从而λ=4是整数,符合题意
是整数,从而λ=4是整数,符合题意
综上可知,当且仅当λ=4时,存在正整数n=2,使等式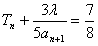 成立。
成立。
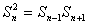
∴
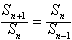
又S1=1≠0,S2=a1+a2=a≠0,
∴{Sn}是首项为1,公比q=a的等比数列
∴
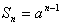
当n≥2时,
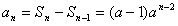
又a1=S1=1
∴
 。
。(2)当a=4,n≥2时
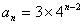
此时
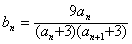
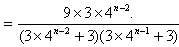
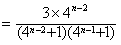
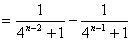 }
}又
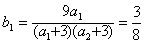
∴
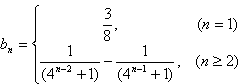
故
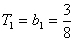
当n≥2时,Tn=b1+b2+…+bn
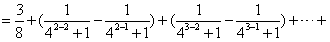
=
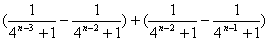
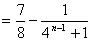
若n=1,则等式
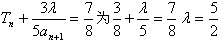 不是整数,不符合题意;
不是整数,不符合题意;若n≥2,则等式
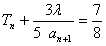 为
为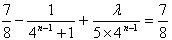
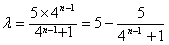
∵λ是整数,
∴
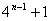 必是5的因数
必是5的因数∵n≥2时, ∴
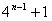 ≥5
≥5当且仅当n=2时,
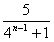 是整数,从而λ=4是整数,符合题意
是整数,从而λ=4是整数,符合题意综上可知,当且仅当λ=4时,存在正整数n=2,使等式
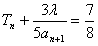 成立。
成立。
练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|