题目内容
3.在△ABC中,已知AB=AC=3,BC=4,P为BC边上的动点,则$\overrightarrow{AP}•(\overrightarrow{AB}+\overrightarrow{AC})$的值为10.分析 根据题意画出图形,结合图形用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出向量$\overrightarrow{AP}$,求$\overrightarrow{AP}•(\overrightarrow{AB}+\overrightarrow{AC})$即可.
解答 解:如图所示,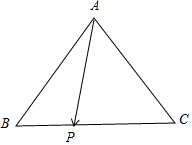
△ABC中,AB=AC=3,BC=4,P为BC边上的动点,
∴$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$
=$\overrightarrow{AB}$+λ$\overrightarrow{BC}$
=$\overrightarrow{AB}$+λ($\overrightarrow{AC}$-$\overrightarrow{AB}$)
=(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AC}$,
∴$\overrightarrow{AP}•(\overrightarrow{AB}+\overrightarrow{AC})$=(1-λ)${\overrightarrow{AB}}^{2}$+λ${\overrightarrow{AC}}^{2}$+$\overrightarrow{AB}$•$\overrightarrow{AC}$
=(1-λ)×32+λ×32+3×3×$\frac{{3}^{2}{+3}^{2}{-4}^{2}}{2×3×3}$
=10.
故答案为:10.
点评 本题考查了平面向量的线性运算与数量积运算问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.将4个不同的小球装入4个不同的盒子,则在至少一个盒子为空的条件下,恰好有两个盒子为空的概率是( )
| A. | $\frac{21}{58}$ | B. | $\frac{12}{29}$ | C. | $\frac{21}{64}$ | D. | $\frac{7}{27}$ |
12.已知某几何体的三视图(单位:cm)如图所示,则该几何体的表面积是( )


| A. | $9+4({\sqrt{2}+\sqrt{5}})c{m^2}$ | B. | $10+2({\sqrt{2}+\sqrt{3}})c{m^2}$ | C. | $11+2({\sqrt{2}+\sqrt{5}})c{m^2}$ | D. | $11+2({\sqrt{2}+\sqrt{3}})c{m^2}$ |
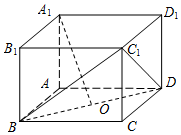 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=$\sqrt{2}$,O为底面中心.
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=$\sqrt{2}$,O为底面中心.