题目内容
给出下列命题:
①存在实数α使sinα•cosα=1成立;
②存在实数α使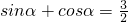 成立;
成立;
③函数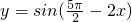 是偶函数;
是偶函数;
④ 是函数
是函数 的图象的一条对称轴的方程;
的图象的一条对称轴的方程;
⑤在△ABC中,若A>B,则sinA>sinB.
其中正确命题的序号是
- A.②③④
- B.③④⑤
- C.①②④
- D.②③⑤
B
分析:①根据正弦二倍角公式sin2α=2sinαcosα对①进行判断;
②利用辅助角公式进行判断;
③函数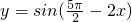 化为余弦,然后在进行判断;
化为余弦,然后在进行判断;
④把x= 代入函数
代入函数 进行判断;
进行判断;
⑤在△ABC中,可判断A,B属于(0,π),再根据A为锐角或钝角两种情况进行说明,进行判断;
解答:①∵sinα•cosα= sin2α=1,∴sin2α=2,显然是不可能的,故①错误;
sin2α=1,∴sin2α=2,显然是不可能的,故①错误;
②∵ =
= ,∴sin(α+
,∴sin(α+ )=
)=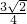 >1,故不存在α使
>1,故不存在α使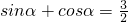 成立;
成立;
③∵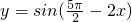 =cos(
=cos( -
- +2x)=cos(2x-2π)=cos2x,∴y是偶函数,故③正确;
+2x)=cos(2x-2π)=cos2x,∴y是偶函数,故③正确;
④把x= 代入得,
代入得, =
= =sin
=sin =-1,∴x=
=-1,∴x= 为y的一条对称轴;故④正确;
为y的一条对称轴;故④正确;
⑤若A>B,当A不超过90°时,显然可得出sinA>sinB,
当A是钝角时,
由于 >π-A>B,可得sin(π-A)=sinA>sinB,
>π-A>B,可得sin(π-A)=sinA>sinB,
即 A>B?sinA>sinB
故选B.
点评:此题主要考查命题的真假的判断及应用,考查的知识点比较多,综合性比较强,是一道中档题;
分析:①根据正弦二倍角公式sin2α=2sinαcosα对①进行判断;
②利用辅助角公式进行判断;
③函数
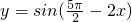 化为余弦,然后在进行判断;
化为余弦,然后在进行判断;④把x=
 代入函数
代入函数 进行判断;
进行判断;⑤在△ABC中,可判断A,B属于(0,π),再根据A为锐角或钝角两种情况进行说明,进行判断;
解答:①∵sinα•cosα=
 sin2α=1,∴sin2α=2,显然是不可能的,故①错误;
sin2α=1,∴sin2α=2,显然是不可能的,故①错误;②∵
 =
= ,∴sin(α+
,∴sin(α+ )=
)=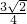 >1,故不存在α使
>1,故不存在α使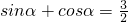 成立;
成立;③∵
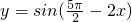 =cos(
=cos( -
- +2x)=cos(2x-2π)=cos2x,∴y是偶函数,故③正确;
+2x)=cos(2x-2π)=cos2x,∴y是偶函数,故③正确;④把x=
 代入得,
代入得, =
= =sin
=sin =-1,∴x=
=-1,∴x= 为y的一条对称轴;故④正确;
为y的一条对称轴;故④正确;⑤若A>B,当A不超过90°时,显然可得出sinA>sinB,
当A是钝角时,
由于
 >π-A>B,可得sin(π-A)=sinA>sinB,
>π-A>B,可得sin(π-A)=sinA>sinB,即 A>B?sinA>sinB
故选B.
点评:此题主要考查命题的真假的判断及应用,考查的知识点比较多,综合性比较强,是一道中档题;

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目