Question

2^-x+x²=5的实根个数为

2

．

Answer 1

分析：问题等价于函数y=2^-x，与函数y=5-x²图象的交点个数，分别作出它们的图象可得．

解答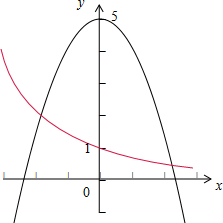：解：2^-x+x²=5的实根个数等价于方程2^-x=5-x²的实根个数
即函数y=2^-x，与函数y=5-x²图象的交点个数
在同一坐标系中作出它们的图象可得图象的交点个数为2
故2^-x+x²=5的实根个数为2
故答案为：2

点评：本题考查方程的根的个数，转化为两函数图象的交点个数是解决问题的关键，属基础题．