题目内容
已知抛物线 的准线与双曲线
的准线与双曲线
 交于
交于 两点,点
两点,点 为抛物线的焦点,若
为抛物线的焦点,若 为直角三角形,则双曲线的离心率是( )
为直角三角形,则双曲线的离心率是( )
A. | B. | C.2 | D.3 |
B
解析试题分析:抛物线 的准线为
的准线为 ,它与双曲线
,它与双曲线
 交于
交于 两点,则坐标为
两点,则坐标为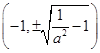 ,抛物线的焦点
,抛物线的焦点 ,因为
,因为 为直角三角形,则有
为直角三角形,则有 ,从而有
,从而有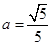 ,
, ,因此
,因此 ,故选择B.
,故选择B.
考点:圆锥曲线的性质.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
(本小题12分)
已知椭圆C的左右焦点坐标分别是(-1,0),(1, 0),离心率
0),离心率 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
(1)求椭圆C的方程;
(2)若圆P恰过坐标原点,求圆P的方程;
点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中点,且∠EPA=∠D1PD,则点P的轨迹是( )
| A.直线 | B.圆 | C.抛物线 | D.双曲线 |
已知 是抛物线
是抛物线 的焦点,
的焦点, 是该抛物线上的两点.若线段
是该抛物线上的两点.若线段 的中点到
的中点到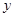 轴的距离为
轴的距离为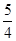 ,则
,则 ( )
( )
| A.2 | B. | C.3 | D.4 |
若双曲线 的离心率为
的离心率为 ,则其渐近线的斜率为( )
,则其渐近线的斜率为( )
A. | B. | C.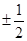 | D. |
已知双曲线
 的渐近线方程为
的渐近线方程为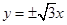 ,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )
,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )
A. | B.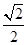 | C. | D.1 |
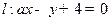 及圆
及圆
 ,求a的值.
,求a的值. B.1 C.
B.1 C. D.
D.