题目内容
已知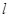 表示一条直线,
表示一条直线,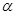 ,
,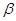 表示两个不重合的平面,有以下三个语句:①
表示两个不重合的平面,有以下三个语句:① ;②
;② ;③
;③ .以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
.以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
A. | B. | C. | D. |
B
解析试题分析:命题①:若 ,则
,则 是正确的命题,如图(1)过直线
是正确的命题,如图(1)过直线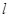 作一个平面
作一个平面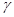 ,
, ,则由
,则由 ,结合线面平行的性质可知
,结合线面平行的性质可知 ,因为
,因为 ,所以
,所以 ,而
,而 ,所以由面面垂直的判定可得
,所以由面面垂直的判定可得 ;命题②:若
;命题②:若 ,则
,则 是错误的命题,如图(2),直线
是错误的命题,如图(2),直线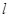 可能在平面
可能在平面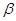 内;命题③:若
内;命题③:若 ,则
,则 是错误的命题,如图(3),直线
是错误的命题,如图(3),直线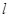 可能在
可能在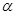 内,如图(4),直线
内,如图(4),直线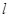 也可能与
也可能与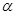 平行,综上可知,三个命题中只有一个命题是正确的,故选B.
平行,综上可知,三个命题中只有一个命题是正确的,故选B.



考点:1.线面平行的性质;2.面面垂直的判定;3.命题真假的判断.

练习册系列答案
相关题目
正方体 -
- 中,
中, 与平面ABCD所成角的余弦值为( )
与平面ABCD所成角的余弦值为( )
A. | B. | C. | D. |
已知一个水平放置的正方形用斜二测画法作出的直观图是一个平行四边形,平行四边形中有一条边长为4,则此正方形的面积是( )
| A.16 | B.64 | C.16或64 | D.以上都不对 |
如图,长方体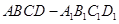 中,
中, ,点
,点 分别是
分别是 的中点,则异面直线
的中点,则异面直线 与
与 所成的角是 ( )
所成的角是 ( )
| A.30° | B.45° | C.60° | D.90° |
如图,已知六棱锥 的底面是正六边形,
的底面是正六边形, 则下列结论正确的是( )
则下列结论正确的是( )
A. |
B.  |
C.直线 ∥ ∥ |
D.直线 所成的角为45° 所成的角为45° |
设a,b是不同的直线,α,β是不同的平面,则下列命题:
①若a⊥b,a∥α,则b∥α;②若a∥α,α⊥β,则a⊥β;
③若a⊥β,α⊥β,则a∥α;④若a⊥b,a⊥α,b⊥β,则α⊥β.
其中正确命题的个数是 ( ).
| A.0 | B.1 | C.2 | D.3 |
在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是 ( ).
| A.30° | B.45° | C.60° | D.90° |




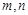 是两条不重合的直线,
是两条不重合的直线,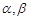 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: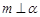 ,
,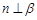 ,且
,且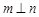 ,则
,则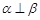 ;
;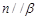 ,且
,且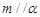 ,
,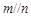 ,则
,则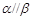 ;
;