题目内容
已知:函数 的最小正周期为3π.
的最小正周期为3π.
(1)求函数f(x)的解析式;
(2)在△ABC中,若f(C)=1,且2sin2B=cosB+cos(A-C),求sinA的值.
解:(1)根据题意,得
 =
= =
= …(3分)
…(3分)
∵函数f(x)的周期为3π,即 ,
,
∴ ,…(5分)
,…(5分)
因此,函数f(x)的解析式是 …(6分)
…(6分)
(2)∵
∴ ,
,
∵C∈(0,π),可得 ,
,
∴ ,可得
,可得 .…(8分)
.…(8分)
∵在Rt△ABC中, ,有2sin2B=cosB+cos(A-C)
,有2sin2B=cosB+cos(A-C)
∴2cos2A-sinA-sinA=0,即sin2A+sinA-1=0,解之得 …(11分)
…(11分)
∵0<sinA<1,∴ .…(12分)
.…(12分)
分析:(1)根据二倍角的三角函数公式和辅助角公式,化简得f(x)= ,再由函数的最小正周期为3π结合三角函数的周期公式,算出
,再由函数的最小正周期为3π结合三角函数的周期公式,算出 即可得到函数f(x)的解析式;
即可得到函数f(x)的解析式;
(2)根据(1)的表达式,解关于C的方程f(C)=1,结合C为三角形的内角算出C= ,因此将等式2sin2B=cosB+cos(A-C)化成关于A的方程,整理得sin2A+sinA-1=0,解之即得sinA的值.
,因此将等式2sin2B=cosB+cos(A-C)化成关于A的方程,整理得sin2A+sinA-1=0,解之即得sinA的值.
点评:本题给出函数y=Asin(ωx+φ)+k的周期,求函数的表达式并依此求三角形ABC的角A的正弦值.着重考查了三角恒等变换、三角函数的图象与性质和同角三角函数的基本关系等知识点,属于中档题.
 =
= =
= …(3分)
…(3分)∵函数f(x)的周期为3π,即
 ,
,∴
 ,…(5分)
,…(5分)因此,函数f(x)的解析式是
 …(6分)
…(6分)(2)∵

∴
 ,
,∵C∈(0,π),可得
 ,
,∴
 ,可得
,可得 .…(8分)
.…(8分)∵在Rt△ABC中,
 ,有2sin2B=cosB+cos(A-C)
,有2sin2B=cosB+cos(A-C)∴2cos2A-sinA-sinA=0,即sin2A+sinA-1=0,解之得
 …(11分)
…(11分)∵0<sinA<1,∴
 .…(12分)
.…(12分)分析:(1)根据二倍角的三角函数公式和辅助角公式,化简得f(x)=
 ,再由函数的最小正周期为3π结合三角函数的周期公式,算出
,再由函数的最小正周期为3π结合三角函数的周期公式,算出 即可得到函数f(x)的解析式;
即可得到函数f(x)的解析式;(2)根据(1)的表达式,解关于C的方程f(C)=1,结合C为三角形的内角算出C=
 ,因此将等式2sin2B=cosB+cos(A-C)化成关于A的方程,整理得sin2A+sinA-1=0,解之即得sinA的值.
,因此将等式2sin2B=cosB+cos(A-C)化成关于A的方程,整理得sin2A+sinA-1=0,解之即得sinA的值.点评:本题给出函数y=Asin(ωx+φ)+k的周期,求函数的表达式并依此求三角形ABC的角A的正弦值.着重考查了三角恒等变换、三角函数的图象与性质和同角三角函数的基本关系等知识点,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知函数y=2sin(ωx+φ)的最小正周是
,直线x=
是该函数图象的一条对称轴,则函数的解析式可以是( )
| π |
| 2 |
| π |
| 6 |
A、y=2sin(4x+
| ||
B、y=2sin(4x-
| ||
C、y=2sin(2x+
| ||
D、y=2sin(2x-
|
 是该函数图象的一条对称轴,则函数的解析式可以是
是该函数图象的一条对称轴,则函数的解析式可以是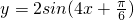
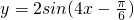
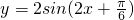
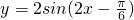
 (其中
(其中 ,
, ,
, )的最大值为2,最小正周
)的最大值为2,最小正周 .
. 的解析式;
的解析式; 的横坐标依次为
的横坐标依次为 ,
, 为坐标原点,求△
为坐标原点,求△ 的
的
 ,函数
,函数 —且最小正周斯为
—且最小正周斯为 ,
, 的最犬值,并写出相应的x的取值集合;
的最犬值,并写出相应的x的取值集合; 中角A,B,C所对的边分别为a,b,c且
中角A,B,C所对的边分别为a,b,c且 ,求b的值.
,求b的值.