Question

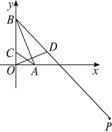
已知点A(2,0),B(0,6),O为坐标原点,

(1)若点C在线段OB上,且∠BAC=,求△ABC的面积;

(2)若原点O关于直线AB的对称点为D,延长BD到P,且|PD|=2|BD|,已知直线l:ax+10y+84-108=0经过点P,求直线l的倾斜角.

Answer 1

直线l的倾斜角为.

解析:

(1)要求△ABC的面积,关键是求C点的坐标,可利用夹角公式先求直线AC的斜率,再写出直线AC的方程,从而可求出C点坐标.

k_AB=-3,

由tan=得k_AC=.所以AC:y= (x-2).

令x=0,得y=1,则C(0,1),

所以S_△ABC=|BC|·|OA|=×5×2=5.

(2)要求直线l的倾斜角,需求参数a的值.由直线l过点P,所以需求出P点的坐标,又P是BD的定比分点,所以还需由对称性求出D点的坐标.

设D点坐标为(x₀,y₀),

因为AB:,即3x+y-6=0,

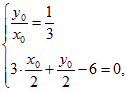所以即所以D(,).

由|PD|=2|BD|,得.

所以

将点P(,)代入l的方程,得a=10.所以k _l= -.

故直线l的倾斜角为.