题目内容
过点（-1，1）作抛物线y=x2+x+1的切线，则切线方程为
x+y=0
x+y=0
．分析：由已知可得点在抛物线上，求其导数可得切线斜率，由点斜式可写方程，整理成一般式即可．
解答：解：经验证点（-1，1）为抛物线y=x2+x+1上的点，
又y′=2x+1，故点（-1，1）处的切线斜率为：y′|x=-1=-1，
由点斜式可得：y-1=-1（x+1），化简得x+y=0
故答案为：x+y=0
又y′=2x+1，故点（-1，1）处的切线斜率为：y′|x=-1=-1，
由点斜式可得：y-1=-1（x+1），化简得x+y=0
故答案为：x+y=0
点评：本题考查函数的切线问题，由导数的几何意义得到切线的斜率是解决问题的关键，属基础题．
练习册系列答案
相关题目
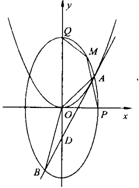已知点D（0，-2），过点D作抛线C1：x2=2py（p＞0）的切线l，切点A在第一象限，如图．
的椭圆
恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若2k1＋k2＝3k，求抛物线C1和椭圆C2的方程．
上的一点A（1，1）作抛物线的切线，分别交x轴于D，交y轴于B，点C在抛物线上，点E在线段AC上，满足
；点F在线段BC上，满足
， 且
=1，线段CD与EF交于点P.当点C在抛物线上移动时，求点P的抛迹方程.
的点到其焦点F的距离;
的值,并证明直线AB的斜率是非零常数.