题目内容
(本题满分16分)数列 ,
, ,
, 满足:
满足: ,
, ,
, .
.
(1)若数列 是等差数列,求证:数列
是等差数列,求证:数列 是等差数列;
是等差数列;
(2)若数列 ,
, 都是等差数列,求证:数列
都是等差数列,求证:数列 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列 是等差数列,试判断当
是等差数列,试判断当 时,数列
时,数列 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
(1)详见解析(2)详见解析(3)数列 成等差数列.
成等差数列.
【解析】
试题分析:(1)证明一个数列为等差数列,一般从等差数列定义出发: ,其中
,其中 为等差数列
为等差数列 的公差(2)同(1),先根据关系式
的公差(2)同(1),先根据关系式 ,
, 解出
解出 ,再从等差数列定义出发
,再从等差数列定义出发 ,其中
,其中 分别为等差数列
分别为等差数列 ,
, 的公差(3)探究性问题,可将条件向目标转化,一方面
的公差(3)探究性问题,可将条件向目标转化,一方面 ,所以
,所以 ,即
,即 ,另一方面
,另一方面 ,所以
,所以 ,整理得
,整理得 ,从而
,从而 ,即数列
,即数列 成等差数列.
成等差数列.
试题解析:证明:(1)设数列 的公差为
的公差为 ,
,
∵ ,
,
∴ ,
,
∴数列 是公差为
是公差为 的等差数列. 4分
的等差数列. 4分
(2)当 时,
时, ,
,
∵ ,∴
,∴ ,∴
,∴ ,
,
∴ ,
,
∵数列 ,
, 都是等差数列,∴
都是等差数列,∴ 为常数,
为常数,
∴数列 从第二项起为等差数列. 10分
从第二项起为等差数列. 10分
(3)数列 成等差数列.
成等差数列.
解法1 设数列 的公差为
的公差为 ,
,
∵ ,
,
∴ ,∴
,∴ , ,
, , ,
,
∴ ,
,
设 ,∴
,∴ ,
,
两式相减得: ,
,
即 ,∴
,∴ ,
,
∴ ,
,
∴ , 12分
, 12分
令 ,得
,得 ,
,
∵ ,∴
,∴ ,∴
,∴ ,
,
∴ ,∴
,∴ ,
,
∴数列 (
( )是公差为
)是公差为 的等差数列, 14分
的等差数列, 14分
∵ ,令
,令 ,
, ,即
,即 ,
,
∴数列 是公差为
是公差为 的等差数列. 16分
的等差数列. 16分
解法2 ∵ ,
, ,
,
令 ,
, ,即
,即 , 12分
, 12分
∴ ,
, ,
,
∴ ,
,
∵数列 是等差数列,∴
是等差数列,∴ ,
,
∴ , 14分
, 14分
∵ ,∴
,∴ ,
,
∴数列 是等差数列. 16分
是等差数列. 16分
考点:等差数列定义
考点分析: 考点1:等差数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 的奇偶性。
的奇偶性。 的实部为
的实部为
 为 .
为 .
 满足
满足 ,求证:
,求证: .
. 中,
中, ,
, ,
, 为梯形
为梯形 =0,
=0, ,
, 为边
为边 上的一个动点,则
上的一个动点,则 的最小值为 .
的最小值为 .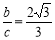 ,
,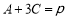 .
.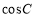 的值;(2)求
的值;(2)求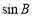 的值;(3)若
的值;(3)若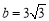 ,求△ABC的面积.
,求△ABC的面积.