题目内容
16.已知函数f(x)=e${\;}^{\frac{{x}^{2}}{a}}$-ax有且只有一个零点,则实数a的取值范围为(-∞,0)∪{$\root{3}{2e}$}.分析 函数f(x)=ex-ax有且只有一个零点可化为函数y=e${\;}^{\frac{{x}^{2}}{a}}$与y=ax的图象有且只有一个交点;分a<0与a>0作图讨论即可.
解答 解:∵函数f(x)=ex-ax有且只有一个零点,
∴函数y=e${\;}^{\frac{{x}^{2}}{a}}$与y=ax的图象有且只有一个交点;
当a<0时,作函数y=ex与y=ax的图象如下,
结合图象知,当a<0时成立,
当a>0时,作函数y=ex与y=ax的图象如下,
相切时成立,
故(e${\;}^{\frac{{x}^{2}}{a}}$)′=$\frac{2x}{a}$e${\;}^{\frac{{x}^{2}}{a}}$=$\frac{{e}^{\frac{{x}^{2}}{a}}}{x}$;
故x2=$\frac{a}{2}$;
且切点(x,e${\;}^{\frac{{x}^{2}}{a}}$)在直线y=ax上知,
${e}^{\frac{1}{2}}$=a•$\sqrt{\frac{a}{2}}$;
故a=$\root{3}{2e}$;
综上所述,实数a的取值范围为(-∞,0)∪{$\root{3}{2e}$}.
故答案为:(-∞,0)∪{$\root{3}{2e}$}.
点评 本题考查了学生作图与用图的能力,同时考查了导数的几何意义的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知x,y∈R,i为虚数单位,若$\frac{x}{1+i}$=1-yi,则x+yi=( )
| A. | 2+i | B. | 1+2i | C. | 1-2i | D. | 2-i |
5.阅读如图所示的框图,运行相应的程序,则输出S的值为( )
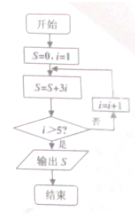

| A. | 30 | B. | 45 | C. | 63 | D. | 84 |
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0))的离心率为$\frac{1}{2}$,点F1、F2分别是椭圆的左、右焦点,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0))的离心率为$\frac{1}{2}$,点F1、F2分别是椭圆的左、右焦点,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切. 如图,梯形ABCD中,DC∥AB,AD=DC=CB=2,AB=4,矩形AEFC中,AE=$\sqrt{3}$,平面AEFC⊥平面ABCD,点G是线段EF的中点
如图,梯形ABCD中,DC∥AB,AD=DC=CB=2,AB=4,矩形AEFC中,AE=$\sqrt{3}$,平面AEFC⊥平面ABCD,点G是线段EF的中点