题目内容
过点M(4,2)作x轴的平行线被曲线C:x2=2py(p>0)截得的弦长为4
.
(I)求p的值;
(II)过点M作直线交抛物线C于A,B两点,过A,B分别作抛物线C的切线l1,l2,记l1,l2的交点为N,当S△ABN=28
时,求点N的坐标.
| 2 |
(I)求p的值;
(II)过点M作直线交抛物线C于A,B两点,过A,B分别作抛物线C的切线l1,l2,记l1,l2的交点为N,当S△ABN=28
| 7 |
分析:(I)由题意可得,点(2
,2)在抛物线x2=2py上,代入可求p,
(II)由题意可设直线AB:y-2=k(x-4),联立抛物线x2=4y,设A(x1,
),B(x2,
)根据方程的根与系数关系可求x1+x2,x1x2,结合弦长公式|AB|=
|x1-x2|=
,利用导数的几何意义可求A,B点处的切线,交点坐标N,由点N到直线AB的距离d=
,代入面积公式可求S△NAB=
|AB|•d=4(
)3,结合已知即可求k
| 2 |
(II)由题意可设直线AB:y-2=k(x-4),联立抛物线x2=4y,设A(x1,
| x12 |
| 4 |
| x22 |
| 4 |
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 2|k2-4k+2| | ||
|
| 1 |
| 2 |
| k2-4k+2 |
解答:解:(I)由题意可得,过M(4,2)所作的直线为y=2截抛物线 弦长为4
∴点(2
,2)在抛物线x2=2py上,…(2分)
代入得8=4p,故p=2.…(5分)
(II)易知直线AB的斜率一定存在,设为k,则AB:y-2=k(x-4)
联立抛物线x2=4y,消元,整理得:x2-4kx+16k-8=0 …(7分)
设A(x1,
),B(x2,
)则x1+x2=4k,x1x2=16k-8
|AB|=
|x1-x2|=
=4
…(9分)
∵y′=
故抛物线在A,B两点处的切线斜率分别为
,
故在A,B点处的切线方程分别为L1y=
x-
,l2:y=
x-
…(11分)
于是,l1与l2的交点坐标为(
,
),即N(2k,4k-2)
点N到直线AB的距离d=
…(12分)
∴S△NAB=
|AB|•d=4(
)3…(13分)
故4(
)3=28
即
=
∴k=-1或k=5,…(14分)
故点N的坐标为(-2,-6)或(10,18).…(15分)
| 2 |
∴点(2
| 2 |
代入得8=4p,故p=2.…(5分)
(II)易知直线AB的斜率一定存在,设为k,则AB:y-2=k(x-4)
联立抛物线x2=4y,消元,整理得:x2-4kx+16k-8=0 …(7分)
设A(x1,
| x12 |
| 4 |
| x22 |
| 4 |
|AB|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
| k2-4k+2 |
∵y′=
| x |
| 2 |
| x1 |
| 2 |
| x2 |
| 2 |
故在A,B点处的切线方程分别为L1y=
| x1 |
| 2 |
| x12 |
| 4 |
| x2 |
| 2 |
| x22 |
| 4 |
于是,l1与l2的交点坐标为(
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
点N到直线AB的距离d=
| 2|k2-4k+2| | ||
|
∴S△NAB=
| 1 |
| 2 |
| k2-4k+2 |
故4(
| k2-4k+2 |
| 7 |
| k2-4k+2 |
| 7 |
∴k=-1或k=5,…(14分)
故点N的坐标为(-2,-6)或(10,18).…(15分)
点评:本题主要考查了利用抛物线的性质求解抛物线的方程,直线与抛物线相交关系的应用,一般思路是联立方程结合方程的根与系数关系进行处理

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
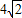 .
.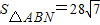 时,求点N的坐标.
时,求点N的坐标. .
. 时,求点N的坐标.
时,求点N的坐标.