题目内容
18.将进货单价为40元的商品按60元一个售出时,能卖出400个.已知该商品每个涨价1元,其销售量就减少10个,为了赚得最大利润,售价应定为( )| A. | 每个70元 | B. | 每个85元 | C. | 每个80元 | D. | 每个75元 |
分析 设销售价为x元,由题意可得销售量就减少10(x-60)个,销售量为1000-10x个,可得利润y=(x-40)(1000-10x),运用配方即可得到所求最大值及对应的x的值.
解答 解:设销售价为x元,由题意可得销售量就减少10(x-60)个,
销售量为400-10(x-60)=1000-10x个,
可得利润y=(x-40)(1000-10x)
=10(-x2+140x-4000)=10[-(x-70)2+900],
当x=70时,y取得最大值9000.
即有为了赚得最大利润,售价应定为70元.
故选:A.
点评 本题考查二次函数的模型应用题的解法,考查函数的最值的求法,注意运用二次函数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.(1+2x)2(1-x)5=${a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$,则a1-a2+a3-a4+a5-a6+a7等于( )
| A. | 32 | B. | -32 | C. | -33 | D. | -31 |
8.已知函数f(x)=mx-m2-1,m>0,x∈R.若a2+b2=1,则$\frac{f(b)}{f(a)}$的取值范围是( )
| A. | [$\frac{\sqrt{7}-4}{3}$,$\frac{\sqrt{7}+4}{3}$] | B. | (0,$\frac{4-\sqrt{7}}{3}$] | C. | [0,$\frac{4+\sqrt{7}}{3}$] | D. | [$\frac{4-\sqrt{7}}{3}$,$\frac{4+\sqrt{7}}{3}$] |
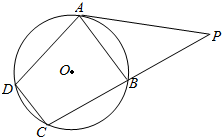 如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.
如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.