题目内容
【题目】已知函数f(x)=(ax﹣1)ex(a≠0,e是自然对数的底数).
(1)若函数f(x)在区间[1,2]上是单调减函数,求实数a的取值范围;
(2)求函数f(x)的极值;
(3)设函数f(x)图象上任意一点处的切线为l,求l在x轴上的截距的取值范围.
【答案】
(1)解:函数f(x)的导函数f'(x)=(ax﹣1+a)ex,
则f'(x)≤0在区间[1,2]上恒成立,且等号不恒成立,
又ex>0,所以ax﹣1+a≤0在区间[1,2]上恒成立,
记g(x)=ax﹣1+a,只需 ![]() ,即
,即 ![]() ,解得
,解得 ![]() 且a≠0
且a≠0
(2)解:由f'(x)=(ax﹣1+a)ex=0,得 ![]() ,
,
①当a<0时,有 ![]() ;
; ![]() ,
,
所以函数f(x)在 ![]() 单调递增,
单调递增, ![]() 单调递减,
单调递减,
所以函数f(x)在 ![]() 取得极大值
取得极大值 ![]() ,没有极小值.
,没有极小值.
②当a>0时,有 ![]() ;
; ![]() ,
,
所以函数f(x)在 ![]() 单调递减,
单调递减, ![]() 单调递增,
单调递增,
所以函数f(x)在 ![]() 取得极小值
取得极小值 ![]() ,没有极大值.
,没有极大值.
综上可知:当a<0时,函数f(x)在 ![]() 取得极大值
取得极大值 ![]() ,没有极小值;
,没有极小值;
当a>0时,函数f(x)在 ![]() 取得极小值
取得极小值 ![]() ,没有极大值
,没有极大值
(3)解:设切点为T(t,(at﹣1)et),
则曲线在点T处的切线l方程为y﹣(at﹣1)et=(at﹣1+a)(x﹣t)et,
当 ![]() 时,切线l的方程为
时,切线l的方程为 ![]() ,其在x轴上的截距不存在.
,其在x轴上的截距不存在.
当 ![]() 时,令y=0,得切线l在x轴上的截距为:
时,令y=0,得切线l在x轴上的截距为:
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ,…(12分)
,…(12分)
当 ![]() 时,
时, 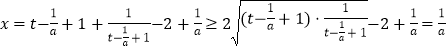 ,
,
当且仅当 ![]() ,即
,即 ![]() 或
或 ![]() 时取等号
时取等号
当 ![]() 时,
时,  ,
,
当且仅当 ![]() ,即
,即 ![]() 或
或 ![]() 时取等号.
时取等号.
所以切线l在x轴上的截距范围是 ![]()
【解析】(1)根据已知可判断函数极值的情况,先找导数为零的点,再判断导数为零的点的左、右两侧的导数符号。(2)根据已知函数求极值求f'(x),令f'(x)=0的求出根并列表检验f'(x)在f'(x)=0的根的附近两侧的符号进而得到结果。(3)利用已知极值求参数,若函数f(x)在点![]() 极值处取得极值,则f'(x)=0,且在该点左右两侧的导数值符号相反。,进而得出切线l在x轴上的截距范围。
极值处取得极值,则f'(x)=0,且在该点左右两侧的导数值符号相反。,进而得出切线l在x轴上的截距范围。
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).