题目内容
集合A满足:若a∈A,则有
∈A;
(1)若集合A为单元素集合,求a和集合A;
(2)是否存在实数a,使集合A中有且仅有两个元素;若存在,求出集合A,若不存在,说明理由;
(3)是否存在实数a,使集合A中有且仅有三个元素;若存在,求出集合A,若不存在,说明理由.
| 2a | 2a+1 |
(1)若集合A为单元素集合,求a和集合A;
(2)是否存在实数a,使集合A中有且仅有两个元素;若存在,求出集合A,若不存在,说明理由;
(3)是否存在实数a,使集合A中有且仅有三个元素;若存在,求出集合A,若不存在,说明理由.
分析:(1)集合A为单元素集合,故a=
,解出即可;
(2)集合A中有且仅有两个元素,故a≠
并且a=
,有解则集合存在,无解则集合不存在;
(3)若集合A中有且仅有三个元素,则a≠
,a≠
=
,a=
=
,有解则集合存在,无解则集合不存在.
| 2a |
| 2a+1 |
(2)集合A中有且仅有两个元素,故a≠
| 2a |
| 2a+1 |
2×
| ||
2×
|
(3)若集合A中有且仅有三个元素,则a≠
| 2a |
| 2a+1 |
2×
| ||
2×
|
| 4a |
| 6a+1 |
2×
| ||
2×
|
| 8a |
| 14a+1 |
解答:解:(1)由于集合A为单元素集合,故a=
,解得a=0或a=
当a=0时,集合={0};当a=
时,集合={
};
(2)集合A中有且仅有两个元素,故a≠
并且a=
=
,
由于方程组无解,故不存在实数a,使集合A中有且仅有两个元素;
(3)若集合A中有且仅有三个元素,则a≠
,a≠
=
,a=
=
,
由于方程组无解,故不存在实数a,使集合A中有且仅有三个元素.
| 2a |
| 2a+1 |
| 1 |
| 2 |
当a=0时,集合={0};当a=
| 1 |
| 2 |
| 1 |
| 2 |
(2)集合A中有且仅有两个元素,故a≠
| 2a |
| 2a+1 |
2×
| ||
2×
|
| 4a |
| 6a+1 |
由于方程组无解,故不存在实数a,使集合A中有且仅有两个元素;
(3)若集合A中有且仅有三个元素,则a≠
| 2a |
| 2a+1 |
2×
| ||
2×
|
| 4a |
| 6a+1 |
2×
| ||
2×
|
| 8a |
| 14a+1 |
由于方程组无解,故不存在实数a,使集合A中有且仅有三个元素.
点评:此题主要考查元素与集合的关系,以方程的求解为载体,考查的知识点比较全面,是一道基础题;

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 ∈M,当a=2时,集合A=________.(用列举法写出集合中的元素)
∈M,当a=2时,集合A=________.(用列举法写出集合中的元素)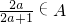 ;
;