题目内容
12.不等式组$\left\{\begin{array}{l}{\sqrt{{x}^{2}-9}≤4}\\{x>0}\end{array}\right.$的解集是{x|0<x≤5}.分析 原不等式组等价于$\left\{\begin{array}{l}{{x}^{2}-9≤16}\\{x>0}\end{array}\right.$,解不等式可得.
解答 解:原不等式组等价于$\left\{\begin{array}{l}{{x}^{2}-9≤16}\\{x>0}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}^{2}≤25}\\{x>0}\end{array}\right.$,
解得0<x≤5,故解集为{x|0<x≤5}
故答案为:{x|0<x≤5}
点评 本题考查无理不等式,等价转化是解决问题的关键,属基础题.

练习册系列答案
相关题目
4.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{-2x},x≤-1}\\{ax+3,x>-1}\end{array}\right.$为单调函数,则实数a的取值范围是( )
| A. | (-1,0] | B. | [-1,0) | C. | (-1,0) | D. | (-∞,-1] |
1.已知A=$\frac{sin(kπ-α)cos[(k-1)π-α]}{sin[(k+1)π+α]cos(kπ+α)}$(k∈Z),则该值构成的集合是( )
| A. | {1,-1,2,-2} | B. | {-1,1} | C. | {-1} | D. | {1,-1,0,2,-2} |
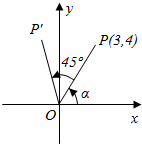 如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.
如图所示,角α终边上一点P的坐标是(3,4),将OP绕原点旋转45°到OP′的位置.试求点P′的坐标.