题目内容
设函数
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）若
，是否存在实数m，使函数f（x）的值域恰为
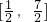？若存在，请求出m的取值；若不存在，请说明理由．
解：（I）由题意可得：
f（x）=2cos2x+2
sinxcosx+m
=1+cos2x+sin2x+m
=2sin（2x+
）+m+1，
所以函数f（x）的最小正周期T=
=π．
（Ⅱ）假设存在实数m符合题意，∵，
∴
…（9分）
∴
…（10分）
又∵
，解得 
…（13分）
∴存在实数，使函数f（x）的值域恰为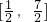…（14分）
分析：（I）由题意可得：f（x）=2sin（2x+）+m+1，再结合周期的计算公式可得答案．
（Ⅱ）假设存在实数m符合题意，由x的范围得：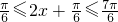
，进而求出函数f（x）的范围，再结合题意可得答案．
点评：本题题考查三角函数的周期性及其求法，以及三角函数的有关性质，两角和与差的正弦函数，二倍角公式，并且考查计算能力，是中档题型．
f（x）=2cos2x+2
sinxcosx+m=1+cos2x+
sin2x+m=2sin（2x+
）+m+1，所以函数f（x）的最小正周期T=
=π．（Ⅱ）假设存在实数m符合题意，∵
，∴
…（9分）∴
…（10分）又∵
，解得 …（13分）∴存在实数
，使函数f（x）的值域恰为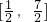…（14分）分析：（I）由题意可得：f（x）=2sin（2x+
）+m+1，再结合周期的计算公式可得答案．（Ⅱ）假设存在实数m符合题意，由x的范围得：
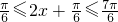，进而求出函数f（x）的范围，再结合题意可得答案．点评：本题题考查三角函数的周期性及其求法，以及三角函数的有关性质，两角和与差的正弦函数，二倍角公式，并且考查计算能力，是中档题型．
练习册系列答案
相关题目
设函数