题目内容
【题目】已知函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,若对任意
,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 和
和![]() 上单调递减; (2)
上单调递减; (2)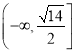 .
.
【解析】
试题(1)求导,讨论导数的正负,导数正得增区间,导数负得减区间. (2)若对任意![]() ,不等式
,不等式![]() 恒成立等价于
恒成立等价于![]() .由(1)可得
.由(1)可得![]() 的值.函数
的值.函数![]() 的图像为开口向下的抛物线,讨论对称轴
的图像为开口向下的抛物线,讨论对称轴![]() 与区间
与区间![]() 的关系可得
的关系可得![]() .根据
.根据![]() 可得关于
可得关于![]() 的不等式.从而可得
的不等式.从而可得![]() 的范围.
的范围.
试题解析:(1)![]() 的定义域是
的定义域是![]() ,
,![]()
由![]() 及
及![]() 得
得![]() ,由
,由![]() 及
及![]() 得
得![]() 或
或![]() ;
;
所以函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 和
和![]() 上单调递减.
上单调递减.
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,问题等价于
恒成立,问题等价于![]()
由(1)可知,在![]() 上,
上,![]() 是函数极小值点,这个极小值是唯一的极值点
是函数极小值点,这个极小值是唯一的极值点
故也是最小值点,所以![]() ,
,![]()
当![]() 时,
时,![]() ;当
;当![]() ,
,![]()
当![]() 时,
时,![]()
问题等价于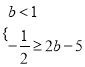 或
或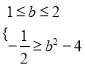 或
或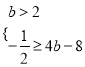
解得![]() 或
或![]() 或
或![]()
即![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是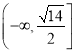 .
.

【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(Ⅱ)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为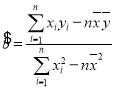 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【题目】某工厂生产![]() ,
,![]() ,
,![]() 三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
普通型 | 精品型 | |
纪念品 | 800 | 200 |
纪念品 |
| 150 |
纪念品 | 500 | 350 |
现采用分层抽样的方法在这一天生产的纪念品中抽取100个,其中有![]() 种纪念品40个.
种纪念品40个.
(1)若再用分层抽样的方法在所有![]() 种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
(2)从![]() 种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,
种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,![]() ,
,![]() ,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求
,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求![]() 的值.
的值.
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.

