题目内容
已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且(1)证明![]() 为定值;
为定值;
(2)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
(1)证明:由已知条件,得F(0,1),λ>0.
设A(x1,y1)、B(x2,y2).
由![]() ,
,
即得(-x1,1-y1)=λ(x2,y2-1),
∴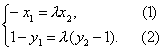
将①式两边平方并把y1=![]() x12,y2=
x12,y2=![]() x22代入得y1=λ2y2, (3)
x22代入得y1=λ2y2, (3)
解②、③式得y1=λ,y2=![]() ,且有x1x2=-λx22=-4λy2=-4.
,且有x1x2=-λx22=-4λy2=-4.
抛物线方程为y=![]() x2.
x2.
求导得y′=![]() x.
x.
所以过抛物线上A、B两点的切线方程分别是y=![]() x1(x-x1)+y1,y=
x1(x-x1)+y1,y=![]() x2(x-x2)+y2,
x2(x-x2)+y2,
即y=![]() x1x-
x1x-![]() x12,y=
x12,y=![]() x2x-
x2x-![]() x22.
x22.
解出两条切线的交点M的坐标为
![]()
所以![]() =(
=(![]() )·(x2-x1,y2-y1)
)·(x2-x1,y2-y1)
=![]() (x22-x12)-2(
(x22-x12)-2(![]() x22-
x22-![]() x12)
x12)
=0.
所以![]() 为定值,其值为0.
为定值,其值为0.
(2)解:由(1)知在△ABM中,FM⊥AB,
因而S=![]() |AB||FM|.
|AB||FM|.
|FM|=![]()
=![]()
=![]()
=![]()
=![]() .
.
因为|AF|、|BF|分别等于A、B到抛物线准线y=-1的距离,
所以|AB|=|AF|+|BF|=y1+y2+2
=λ+![]() +2=(
+2=(![]() )2.
)2.
于是S=![]() |AB||FM|=
|AB||FM|=![]() (
(![]() )3,
)3,
由![]() ≥2,知S≥4,
≥2,知S≥4,
且当λ=1时,S取得最小值4.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点.
已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点. (2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.
(2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F. (2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.
(2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.