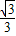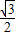题目内容
已知OA、OB、OC三射线两两成60°角,则OA与平面OBC所成角的余弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由已知中OA、OB、OC三射线两两成60°角,令OA在平面OBC上的射影为OD,则∠AOD即为OA与平面OBC所成角,由三垂线定理得cos∠AOB=cos∠AOD•cos∠DOB,我们易得到OA与平面OBC所成角的余弦值.
解答:解:∵OA、OB、OC三射线两两成60°角
令OA在平面OBC上的射影为OD,
则∠AOD即为OA与平面OBC所成角
∵∠AOB=60°,∠DOB=30°,
由三余弦定理得cos∠AOB=cos∠AOD•cos∠DOB
∴cos∠AOD=
故选B
令OA在平面OBC上的射影为OD,
则∠AOD即为OA与平面OBC所成角
∵∠AOB=60°,∠DOB=30°,
由三余弦定理得cos∠AOB=cos∠AOD•cos∠DOB
∴cos∠AOD=
| ||
| 3 |
故选B
点评:本题考查的知识点是直线与平面所成的角,其中三垂线定理:cos∠AOB=cos∠AOD•cos∠DOB,可以简化解答过程.

练习册系列答案
相关题目
已知
•x2+
•x-
=
(x∈R),其中A、B、C三点共线,则满足条件的x( )
| OA |
| OB |
| OC |
| 0 |
| A、不存在 | B、有一个 |
| C、有两个 | D、以上情况均有可能 |