题目内容
1.如图,已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{m}$=1(0<m<4)的左顶点为A,点N的坐标为(1,0).若椭圆C上存在点M(点M异于点A),使得点A关于点M对称的点P满足PO=$\sqrt{2}$PN,则实数m的最大值为$\frac{1}{2}$.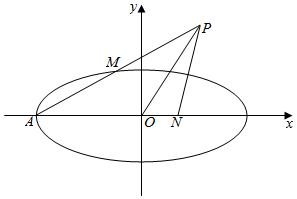
分析 设M(x0,y0),则$\frac{{{x}_{0}}^{2}}{4}$+$\frac{{{y}_{0}}^{2}}{m}$=1,因为PO=$\sqrt{2}$PN,所以可得:2x02+2y02=1.两式联立,表示出m,利用二次函数的图象和性质即可得出结论.
解答 解:依题意,M是线段AP的中点,A(-2,0),
设M(x0,y0),则 $\frac{{{x}_{0}}^{2}}{4}$+$\frac{{{y}_{0}}^{2}}{m}$=1①,由题意知-2<x0<2.
因为M是线段AP的中点,所以P(2x0+2,2y0).
因为PO=$\sqrt{2}$PN,N的坐标为(1,0).
所以$\sqrt{(2{x}_{0}+2)^{2}+(2{y}_{0})^{2}}$=$\sqrt{2}$$\sqrt{(2{x}_{0}+1)^{2}+(2{y}_{0})^{2}}$.
整理可得:2x02+2y02=1,②
由①②消去y0,整理可得m=$\frac{2-4{{x}_{0}}^{2}}{4-{{x}_{0}}^{2}}$=4-$\frac{14}{4-{{x}_{0}}^{2}}$,
利用二次函数的图象和性质可得:当x0=0时,m的最大值是$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查椭圆方程,考查二次函数的图象和性质的运用,考查学生分析解决问题的能力,正确表示点的坐标是关键.

练习册系列答案
相关题目
11.下列命题中,正确的是( )
| A. | 如果直线l与平面α内无数条直线成异面直线,则l∥α | |
| B. | 如果直线l与平面α内无数条直线平行,则l∥α | |
| C. | 如果直线l与平面α内无数条直线成异面直线,则l?α | |
| D. | 如果一条直线与一个平面平行,则该直线平行于这个平面内的所有直线 | |
| E. | 如果一条直线上有无数个点不在平面内,则这条直线与这个平面平行 |
10.掷一枚均匀的硬币4次,则出现“3次正面朝上,1次反面朝上”的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
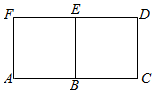 如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:
如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出: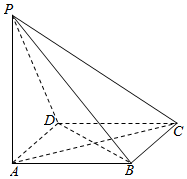 如图,四棱锥P-ABCD的底面为正方形,且PA⊥底面ABCD中,AB=1,PA=2.
如图,四棱锥P-ABCD的底面为正方形,且PA⊥底面ABCD中,AB=1,PA=2.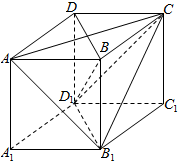 如图,棱长为1的正方体ABCD-A1B1C1D1中,
如图,棱长为1的正方体ABCD-A1B1C1D1中,