题目内容
若函数y=ax+1在
上有且只有一个零点，则实数a的取值范围是________．
（2，+∞）∪（-∞，-
）
分析：由函数零点判定定理可得f（
）f（2）=（a+1）（2a+1）＜0，解此一元二次不等式求出实数a的取值范围．
解答：∵函数y=f（x）=ax+1在上是单调函数，有且只有一个零点，
∴f（）f（2）=（a+1）（2a+1）＜0，
解得 a＞2或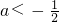
，故实数a的取值范围是（2，+∞）∪（-∞，-），
故答案为 （2，+∞）∪（-∞，-）．
点评：本题考查函数零点的定义以及函数零点判定定理的应用，属于基础题．
）分析：由函数零点判定定理可得f（
）f（2）=（a+1）（2a+1）＜0，解此一元二次不等式求出实数a的取值范围．解答：∵函数y=f（x）=ax+1在
上是单调函数，有且只有一个零点，∴f（
）f（2）=（a+1）（2a+1）＜0，解得 a＞2或
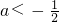，故实数a的取值范围是（2，+∞）∪（-∞，-），故答案为 （2，+∞）∪（-∞，-
）．点评：本题考查函数零点的定义以及函数零点判定定理的应用，属于基础题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目