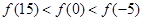题目内容
设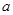 为实数,函数
为实数,函数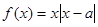 ,
,
(1)当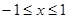 时,讨论
时,讨论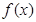 的奇偶性;
的奇偶性;
(2)当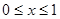 时,求
时,求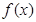 的最大值.
的最大值.
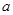 为实数,函数
为实数,函数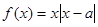 ,
,(1)当
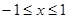 时,讨论
时,讨论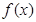 的奇偶性;
的奇偶性;(2)当
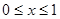 时,求
时,求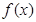 的最大值.
的最大值.(1)当 时,函数
时,函数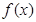 为奇函数;当
为奇函数;当 时,函数
时,函数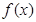 既不是奇函数又不是偶函数.(2)综上:当
既不是奇函数又不是偶函数.(2)综上:当 时,
时, ;当
;当 时,
时, ;当
;当 时,
时, ;
;
 时,函数
时,函数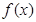 为奇函数;当
为奇函数;当 时,函数
时,函数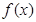 既不是奇函数又不是偶函数.(2)综上:当
既不是奇函数又不是偶函数.(2)综上:当 时,
时, ;当
;当 时,
时, ;当
;当 时,
时, ;
;试题分析:(1)因为函数解析式中的绝对值受
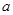 取值的约束,所以应对
取值的约束,所以应对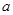 的值进行分类讨论,当
的值进行分类讨论,当 时,也可检验
时,也可检验 与
与 的值关系来判断函数的奇偶;(2)对
的值关系来判断函数的奇偶;(2)对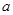 与自变量
与自变量 的范围进行分类讨论
的范围进行分类讨论试题解析:(1)当时
 ,
, ,
,此时
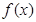 为奇函数. 3分
为奇函数. 3分当
 时,
时, ,
, ,
,由
 且
且 ,
,此时
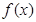 既不是奇函数又不是偶函数 6分
既不是奇函数又不是偶函数 6分 (2)当
 时,
时,∵
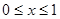 时,
时, 为增函数,
为增函数,∴
 时,
时, . 8分
. 8分当
 时,
时,∵
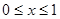 ,
,∴
 ,其图象如图所示: 10分
,其图象如图所示: 10分
①当
 ,即
,即 时,
时, . 11分
. 11分 ②当
 ,即
,即 时,
时, 12分
12分③当
 ,即
,即 时,
时, 13分
13分综上:当
 时,
时, ;
;当
 时,
时, ;
;当
 时,
时, ; 14分
; 14分
练习册系列答案
相关题目
 ,其中常数
,其中常数 满足
满足
 ,判断函数
,判断函数 的单调性;
的单调性; ,求
,求 时的
时的 的取值范围.
的取值范围.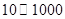 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金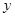 (单位:万元)随投资收益
(单位:万元)随投资收益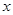 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于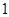 万元,同时不超过投资收益的
万元,同时不超过投资收益的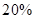 .
.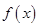 ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型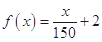 ; ②
; ②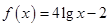
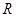 上的函数
上的函数 ,有如下四个命题:
,有如下四个命题: ,则函数
,则函数 则函数
则函数 则函数
则函数 的图象向右平移
的图象向右平移 个单位后关于
个单位后关于 对称,当
对称,当 时,
时, <0恒成立,设
<0恒成立,设 ,
, ,
, ,则
,则 的大小关系为( )
的大小关系为( )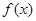 是定义在
是定义在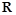 上的奇函数,且当
上的奇函数,且当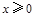 时,
时,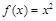 ,若对任意
,若对任意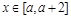 ,不等式
,不等式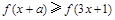 恒成立,则实数
恒成立,则实数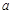 的取值范围是 .
的取值范围是 .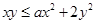 对于
对于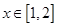 ,
,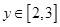 恒成立,则实数
恒成立,则实数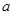 的取值范围是___________.
的取值范围是___________. 在
在 上是增函数,
上是增函数, ,若
,若 ,则x的取值范围是________________.
,则x的取值范围是________________.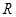 上的偶函数
上的偶函数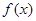 满足
满足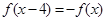 且在区间
且在区间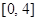 上是增函数则( )
上是增函数则( )