题目内容
已知函数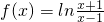
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)对于x∈[2,6], 恒成立,求实数m取值范围.
恒成立,求实数m取值范围.
解:(1)由 ,解得x<-1或x>1,∴定义域为(-∞,-1)∪(1,+∞)(2分)
,解得x<-1或x>1,∴定义域为(-∞,-1)∪(1,+∞)(2分)
当x∈(-∞,-1)∪(1,+∞)时,
∴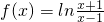 是奇函数. ….(5分)
是奇函数. ….(5分)
(2)由x∈[2,6]时, 恒成立,
恒成立,
∴ ,
,
∵x∈[2,6],∴0<m<(x+1)(7-x)在x∈[2,6]成立…(8分)
令g(x)=(x+1)(7-x)=-(x-3)2+16,x∈[2,6],
由二次函数的性质可知x∈[2,3]时函数单调递增,x∈[3,6]时函数单调递减,
∴x∈[2,6]时,g(x)min=g(6)=7
∴0<m<7….(12分)
分析:(1)利用真数大于0,可得函数的定义域,利用奇偶函数的定义,可得函数f(x)的奇偶性;
(2)将问题转化为0<m<(x+1)(7-x)在x∈[2,6]成立,利用二次函数的性质,即可求得结论.
点评:本题考查函数的性质,考查恒成立问题,解题的关键是确定函数的定义域,利用奇偶性的定义,熟练掌握二次函数的性质.
 ,解得x<-1或x>1,∴定义域为(-∞,-1)∪(1,+∞)(2分)
,解得x<-1或x>1,∴定义域为(-∞,-1)∪(1,+∞)(2分)当x∈(-∞,-1)∪(1,+∞)时,

∴
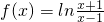 是奇函数. ….(5分)
是奇函数. ….(5分)(2)由x∈[2,6]时,
 恒成立,
恒成立,∴
 ,
,∵x∈[2,6],∴0<m<(x+1)(7-x)在x∈[2,6]成立…(8分)
令g(x)=(x+1)(7-x)=-(x-3)2+16,x∈[2,6],
由二次函数的性质可知x∈[2,3]时函数单调递增,x∈[3,6]时函数单调递减,
∴x∈[2,6]时,g(x)min=g(6)=7
∴0<m<7….(12分)
分析:(1)利用真数大于0,可得函数的定义域,利用奇偶函数的定义,可得函数f(x)的奇偶性;
(2)将问题转化为0<m<(x+1)(7-x)在x∈[2,6]成立,利用二次函数的性质,即可求得结论.
点评:本题考查函数的性质,考查恒成立问题,解题的关键是确定函数的定义域,利用奇偶性的定义,熟练掌握二次函数的性质.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)