题目内容
已知f(x)=sinxcosx-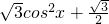 ,x∈[0,π],函数g(x)=f(x)-m有两个不相等的零点.
,x∈[0,π],函数g(x)=f(x)-m有两个不相等的零点.
(1)求m的取值范围;
(2)求函数g(x)的两零点之和.
解:(1)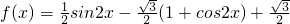 =
=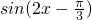 . 又x∈[0,π],故
. 又x∈[0,π],故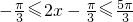 .
.
在同一坐标系中,作出函数y=sinu 的图象和直线y=m的图象.如图易知,
的图象和直线y=m的图象.如图易知,
两图象有两个公共点时,m的取值范围为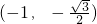 ∪
∪ .
.
又由于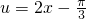 是单调函数,x与u是一一对应,故上述范围即为所求.
是单调函数,x与u是一一对应,故上述范围即为所求.

(2)由图知,直线y= 分函数y=sinu
分函数y=sinu 图象成上下两部分,上、下两部分的图象分别关于直线u=
图象成上下两部分,上、下两部分的图象分别关于直线u=
与u= 对称,故函数g(x)的两零点之和须分两种情况讨论求解,即分
对称,故函数g(x)的两零点之和须分两种情况讨论求解,即分 与
与 .
.
当 时,函数y=sinu
时,函数y=sinu 的图象为直线y=
的图象为直线y= 的上面部分,它关于直线u=
的上面部分,它关于直线u= 对称,
对称,
于是sinu=m的两根之和为:u1+u2=2× =π,从而函数g(x)的两零点之和为:
=π,从而函数g(x)的两零点之和为: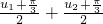 =
= ;
;
当 时,函数y=sinu
时,函数y=sinu 的图象为直线y=
的图象为直线y= 的下面部分,它关于直线u=
的下面部分,它关于直线u= 对称,
对称,
于是sinu=m的两根之和为:u1+u2=2× =3π,从而函数g(x)的两零点之和为:
=3π,从而函数g(x)的两零点之和为: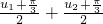 =
= .
.
综上所述,函数两零点之和为 或
或 .
.
分析:(1)化简 f(x)=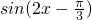 ,在同一坐标系中,作出函数y=sinu
,在同一坐标系中,作出函数y=sinu 的图象和直线y=m的图象,
的图象和直线y=m的图象,
如图易知,满足条件的 m的取值范围为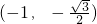 ∪
∪ .
.
(2)当 时,函数y=sinu
时,函数y=sinu 的图象关于直线u=
的图象关于直线u= 对称,g(x)的两零点之和为:
对称,g(x)的两零点之和为: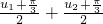 =
= ;当
;当 时,函数y=sinu
时,函数y=sinu 的图象关于直线u=
的图象关于直线u= 对称,
对称,
函数g(x)的两零点之和为: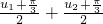 =
= .
.
点评:本题考查两角和差的正弦公式,正弦函数的单调性,对称性,体现了数形结合的数学思想,在同一坐标系中,作出函数y=sinu 的图象和直线y=m的图象,是解题的关键.
的图象和直线y=m的图象,是解题的关键.
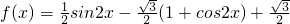 =
=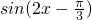 . 又x∈[0,π],故
. 又x∈[0,π],故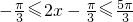 .
.在同一坐标系中,作出函数y=sinu
 的图象和直线y=m的图象.如图易知,
的图象和直线y=m的图象.如图易知,两图象有两个公共点时,m的取值范围为
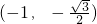 ∪
∪ .
.又由于
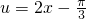 是单调函数,x与u是一一对应,故上述范围即为所求.
是单调函数,x与u是一一对应,故上述范围即为所求.
(2)由图知,直线y=
 分函数y=sinu
分函数y=sinu 图象成上下两部分,上、下两部分的图象分别关于直线u=
图象成上下两部分,上、下两部分的图象分别关于直线u=
与u=
 对称,故函数g(x)的两零点之和须分两种情况讨论求解,即分
对称,故函数g(x)的两零点之和须分两种情况讨论求解,即分 与
与 .
.当
 时,函数y=sinu
时,函数y=sinu 的图象为直线y=
的图象为直线y= 的上面部分,它关于直线u=
的上面部分,它关于直线u= 对称,
对称,于是sinu=m的两根之和为:u1+u2=2×
 =π,从而函数g(x)的两零点之和为:
=π,从而函数g(x)的两零点之和为: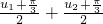 =
= ;
;当
 时,函数y=sinu
时,函数y=sinu 的图象为直线y=
的图象为直线y= 的下面部分,它关于直线u=
的下面部分,它关于直线u= 对称,
对称,于是sinu=m的两根之和为:u1+u2=2×
 =3π,从而函数g(x)的两零点之和为:
=3π,从而函数g(x)的两零点之和为: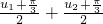 =
= .
.综上所述,函数两零点之和为
 或
或 .
.分析:(1)化简 f(x)=
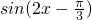 ,在同一坐标系中,作出函数y=sinu
,在同一坐标系中,作出函数y=sinu 的图象和直线y=m的图象,
的图象和直线y=m的图象,如图易知,满足条件的 m的取值范围为
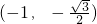 ∪
∪ .
.(2)当
 时,函数y=sinu
时,函数y=sinu 的图象关于直线u=
的图象关于直线u= 对称,g(x)的两零点之和为:
对称,g(x)的两零点之和为: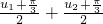 =
= ;当
;当 时,函数y=sinu
时,函数y=sinu 的图象关于直线u=
的图象关于直线u= 对称,
对称,函数g(x)的两零点之和为:
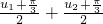 =
= .
.点评:本题考查两角和差的正弦公式,正弦函数的单调性,对称性,体现了数形结合的数学思想,在同一坐标系中,作出函数y=sinu
 的图象和直线y=m的图象,是解题的关键.
的图象和直线y=m的图象,是解题的关键. 
练习册系列答案
相关题目
已知f(x)=sin(x+
),g(x)=cos(x-
),则f(x)的图象( )
| π |
| 2 |
| π |
| 2 |
| A、与g(x)的图象相同 | ||
| B、与g(x)的图象关于y轴对称 | ||
C、向左平移
| ||
D、向右平移
|