题目内容
(2013•延庆县一模)已知函数f(x)=-2a2lnx+
x2+ax(a∈R).
(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))的切线方程;
(Ⅱ)讨论函数f(x)的单调性.
| 1 | 2 |
(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))的切线方程;
(Ⅱ)讨论函数f(x)的单调性.
分析:可得函数的定义域和导函数,(Ⅰ)代入a=1可得f(1),和f'(1),进而可得切线方程;(Ⅱ)可得导函数为f′(x)=
,分a=0和a>0即a<0三类分别求得导数的正负情况,进而可得单调性.
| (x+2a)(x-a) |
| x |
解答:解:函数f(x)的定义域为(0,+∞),f′(x)=-
+x+a.…(2分)
(Ⅰ) 当a=1时,f(1)=
,f'(1)=-2+1+1=0,
所以曲线y=f(x)在点(1,f(1))的切线方程为y=
.…(5分)
(Ⅱ)f′(x)=
=
,…(6分)
(1)当a=0时,f'(x)=x>0,f(x)在定义域为(0,+∞)上单调递增,…(7分)
(2)当a>0时,令f'(x)=0,得x1=-2a(舍去),x2=a,
当x变化时,f'(x),f(x)的变化情况如下:
此时,f(x)在区间(0,a)单调递减,在区间(a,+∞)上单调递增; …(10分)
(3)当a<0时,令f'(x)=0,得x1=-2a,x2=a(舍去),
当x变化时,f'(x),f(x)的变化情况如下:
此时,f(x)在区间(0,-2a)单调递减,在区间(-2a,+∞)上单调递增.…(13分)
| 2a2 |
| x |
(Ⅰ) 当a=1时,f(1)=
| 3 |
| 2 |
所以曲线y=f(x)在点(1,f(1))的切线方程为y=
| 3 |
| 2 |
(Ⅱ)f′(x)=
| x2+ax-2a2 |
| x |
| (x+2a)(x-a) |
| x |
(1)当a=0时,f'(x)=x>0,f(x)在定义域为(0,+∞)上单调递增,…(7分)
(2)当a>0时,令f'(x)=0,得x1=-2a(舍去),x2=a,
当x变化时,f'(x),f(x)的变化情况如下:
| x | (0,a) | a | (a,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 减 | 极小值 | 增 |
(3)当a<0时,令f'(x)=0,得x1=-2a,x2=a(舍去),
当x变化时,f'(x),f(x)的变化情况如下:
| x | (0,-2a) | -2a | (-2a,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 减 | 极小值 | 增 |
点评:本题考查利用导数研究函数的单调性,涉及切线方程的求解,属中档题.

练习册系列答案
相关题目
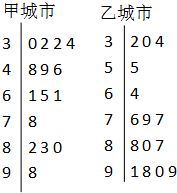 (2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
(2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重: (2013•延庆县一模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.
(2013•延庆县一模)如图,四棱锥P-ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥底面ABCD,PA=AB=2,E为PA的中点.