题目内容
 如图,为了解某海域海底构造,在海平面内一条直线上的A、B、C三点进行测量.已知AB=50 m,BC=120 m,于A处测得水深AD=80 m,于B处测得水深BE=200 m,于C处测得水深CF=110 m,求∠DEF的余弦值.
如图,为了解某海域海底构造,在海平面内一条直线上的A、B、C三点进行测量.已知AB=50 m,BC=120 m,于A处测得水深AD=80 m,于B处测得水深BE=200 m,于C处测得水深CF=110 m,求∠DEF的余弦值.
分析:先利用勾股定理分别求得DF,DE和EF,进而利用余弦定理求得cos∠DEF的值.
解答: 解:如图作DM∥AC交BE于N,交CF于M.
解:如图作DM∥AC交BE于N,交CF于M.
DF=
=
=10
(m),
DE=
=
=130(m),
EF=
=
=150(m).
在△DEF中,由余弦定理的变形公式,得
cos∠DEF=
=
=
.
 解:如图作DM∥AC交BE于N,交CF于M.
解:如图作DM∥AC交BE于N,交CF于M.DF=
| MF2+DM2 |
| 302+1702 |
| 298 |
DE=
| DN2+EN2 |
| 502+1202 |
EF=
| (BE-FC)2+BC2 |
| 902+1202 |
在△DEF中,由余弦定理的变形公式,得
cos∠DEF=
| DE2+EF2-DF2 |
| 2DE•EF |
| 1302+1502-102×298 |
| 2×130×150 |
| 16 |
| 65 |
点评:本题主要考查了解三角形问题的实际应用.综合考查了三角形问题中勾股定理,余弦定理的灵活运用.

练习册系列答案
相关题目
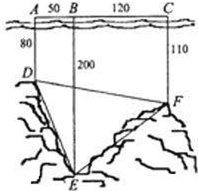 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,求∠DEF的余弦值.
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,求∠DEF的余弦值.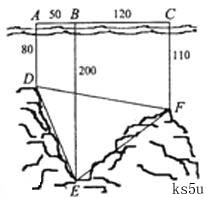 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知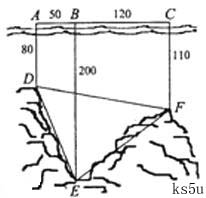 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知 ,
, ,于A处测得水深
,于A处测得水深 ,于B处测得水深
,于B处测得水深 ,于C处测得水深
,于C处测得水深 ,求∠DEF的余弦值。
,求∠DEF的余弦值。
