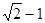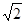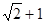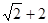题目内容
过抛物线 的焦点
的焦点 的直线与抛物线交于A、B两点,抛物线准线与x轴交于C点,若
的直线与抛物线交于A、B两点,抛物线准线与x轴交于C点,若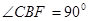 ,则|AF|-|BF|的值为( )
,则|AF|-|BF|的值为( )
A.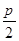 B.
B.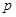 C.
C.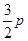 D.
D.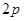
D
解析试题分析:F(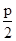 ,0),C(-
,0),C(-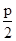 ,0)设AB方程为:y=k(x-
,0)设AB方程为:y=k(x-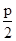 )( k一定存在)
)( k一定存在)
与 联立可得
联立可得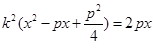 ,
,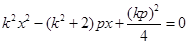
设两交点为A(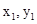 ),B(
),B( ),(不妨设
),(不妨设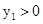 )由韦达定理
)由韦达定理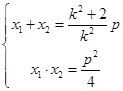
由∠CBF=90°得
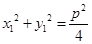 ,
,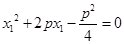 ,
,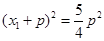
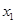 =
=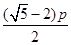 或
或 (舍)
(舍) ,
,
即k=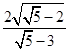 ,所以
,所以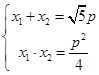
则由|AF|-|BF|=(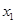 +
+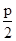 )-(
)-(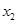 +
+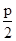 )=
)=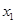 -
-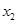 =
=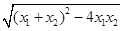 =
=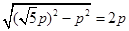
故选D。
考点:本题主要考查直线与抛物线的位置关系,直线的斜率,直线方程。
点评:中档题,本题式子变形较为复杂,需要耐心细致。灵活运用韦达定理及向量垂直,得到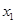 是进一步解题的关键。
是进一步解题的关键。

练习册系列答案
相关题目
与椭圆 共焦点且过点(5,-2)的双曲线标准方程是
共焦点且过点(5,-2)的双曲线标准方程是
A. | B. | C. | D. |
设 ,则双曲线
,则双曲线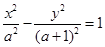 的离心率
的离心率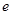 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C.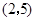 | D. |
双曲线 (p>0)的左焦点在抛物线y2=2px的准线上,则该双曲线的离
(p>0)的左焦点在抛物线y2=2px的准线上,则该双曲线的离
心率( )
| A.1 | B. | C. | D.2 |
 ="1" (a>b>0) 的左、右焦点分别为F1、F2,P为椭圆M上任一点,且
="1" (a>b>0) 的左、右焦点分别为F1、F2,P为椭圆M上任一点,且 的最大值的取值范围是
的最大值的取值范围是 ,其中
,其中 . 则椭圆M的离心率e的取值范围是( ).
. 则椭圆M的离心率e的取值范围是( ).



 的焦点
的焦点 恰好是曲线
恰好是曲线 的右焦点,且曲线
的右焦点,且曲线 与曲线
与曲线 交点连线过点
交点连线过点



 ,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且
,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )
 B、
B、 C、
C、 D、
D、
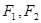 .分别是双曲线
.分别是双曲线 的左,右焦点,若在双曲线右支上存在点P,满足
的左,右焦点,若在双曲线右支上存在点P,满足 ,且
,且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )


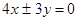
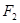 作垂直于实轴的直线,交双曲线于P、Q,
作垂直于实轴的直线,交双曲线于P、Q,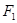 是另一焦点,若∠
是另一焦点,若∠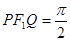 ,则双曲线的离心率
,则双曲线的离心率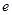 等于( )
等于( )