题目内容

10．设f（x）=x-sinx，则f（x）（　　）
A．既是奇函数又是减函数B．既是奇函数又是增函数
C．是有零点的减函数D．是没有零点的奇函数

分析 利用函数的奇偶性的定义判断f（x）为奇函数，再利用导数研究函数的单调性，从而得出结论．

解答 解：由于f（x）=x-sinx的定义域为R，且满足f（-x）=-x+sinx=-f（x），
可得f（x）为奇函数．
再根据f′（x）=1-cosx≥0，可得f（x）为增函数，
故选：B．

点评 本题主要考查函数的奇偶性的判断方法，利用导数研究函数的单调性，属于基础题．

练习册系列答案
相关题目
20．已知函数f（x）=x3+ax+$\frac{1}{4}$，g（x）=-lnx
（i）当 a为何值时，x轴为曲线y=f（x）的切线；
（ii）用min {m，n }表示m，n中的最小值，设函数h（x）=min { f（x），g（x）}（x＞0），讨论h（x）零点的个数．
1．执行如图所示的程序框图，则输出s的值为（　　）
A．$\frac{3}{4}$B．$\frac{5}{6}$C．$\frac{11}{12}$D．$\frac{25}{24}$
18．某食品保鲜时间y（单位：小时）与储藏温度x（单位：℃）满足函数关系y=ekx+b （e=2.718…为自然对数的底数，k，b为常数）．若该食品在0℃的保鲜时间是192小时，在22℃的保鲜时间是48小时，则该食品在33℃的保鲜时间是（　　）
A．16小时B．20小时C．24小时D．28小时
5．已知A、B、C为△ABC的内角，tanA，tanB是关于方程x2+$\sqrt{3}$px-p+1=0（p∈R）两个实根．
（Ⅰ）求C的大小
（Ⅱ）若AB=3，AC=$\sqrt{6}$，求p的值．
15．如图，在直角梯形ABCD中，AD∥BC，∠BAD=$\frac{π}{2}$，AB=BC=$\frac{1}{2}$AD=a，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到如图2中△A1BE的位置，得到四棱锥A1-BCDE．

（Ⅰ）证明：CD⊥平面A1OC；
（Ⅱ）当平面A1BE⊥平面BCDE时，四棱锥A1-BCDE的体积为36$\sqrt{2}$，求a的值．
2．阅读如图所示的程序框图，运行相应的程序，若输入x的值为1，则输出y的值为（　　）
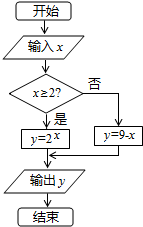
A．2B．7C．8D．128
19．已知函数f（x）=lnx-$\frac{（x-1）^{2}}{2}$．
（Ⅰ）求函数f（x）的单调增区间；
（Ⅱ）证明；当x＞1时，f（x）＜x-1；
（Ⅲ）确定实数k的所有可能取值，使得存在x0＞1，当x∈（1，x0）时，恒有f（x）＞k（x-1）．
20．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点为F（2，0），且双曲线的渐近线与圆（x-2）2+y2=3相切，则双曲线的方程为（　　）
A．$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{13}$=1B．$\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{9}$=1C．$\frac{{x}^{2}}{3}$-y2=1D．x2-$\frac{{y}^{2}}{3}$=1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网