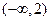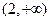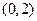题目内容
若x、y、z∈R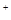 且x+y+z=1,求(
且x+y+z=1,求(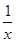 -1)(
-1)( 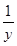 -1)(
-1)( 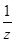 -1)的最小值。
-1)的最小值。
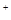 且x+y+z=1,求(
且x+y+z=1,求(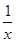 -1)(
-1)( 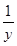 -1)(
-1)( 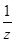 -1)的最小值。
-1)的最小值。9
由已知x+y+z=1而联想到,只有将所求式变形为含代数式x+y+z,或者运用均值不等式后含xyz的形式。所以,关键是将所求式进行合理的变形,即等价转化。
解:(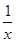 -1)(
-1)( 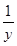 -1)(
-1)( 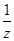 -1)=
-1)=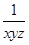 (1-x)(1-y)(1-z)
(1-x)(1-y)(1-z)
=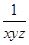 (1-x-y-z+xy+yz+zx-xyz)=
(1-x-y-z+xy+yz+zx-xyz)=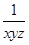 (xy+yz+zx-xyz)
(xy+yz+zx-xyz)
=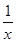 +
+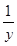 +
+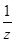 -1≥3
-1≥3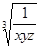 -1=
-1=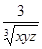 -1≥
-1≥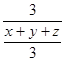 -1=9
-1=9
解:(
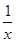 -1)(
-1)( 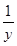 -1)(
-1)( 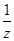 -1)=
-1)=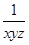 (1-x)(1-y)(1-z)
(1-x)(1-y)(1-z)=
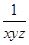 (1-x-y-z+xy+yz+zx-xyz)=
(1-x-y-z+xy+yz+zx-xyz)=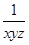 (xy+yz+zx-xyz)
(xy+yz+zx-xyz)=
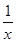 +
+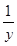 +
+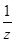 -1≥3
-1≥3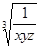 -1=
-1=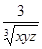 -1≥
-1≥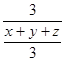 -1=9
-1=9
练习册系列答案
相关题目
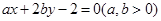 始终平分圆
始终平分圆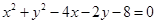 的周长,则
的周长,则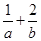 的最小值为 ( )
的最小值为 ( )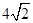
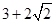
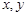 满足
满足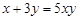 ,则
,则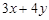 的最小值是( )
的最小值是( )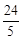
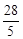
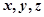 均为正实数,则
均为正实数,则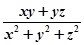 的最大值是 _____ .
的最大值是 _____ .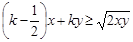 恒成立,则实数
恒成立,则实数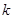 的最小值是 ( )
的最小值是 ( )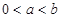 ,则下列不等式中正确的是( )
,则下列不等式中正确的是( )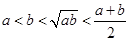
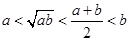
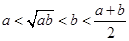
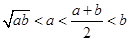
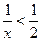 的解集是( )
的解集是( )