题目内容
(本小题满分14分)
函数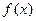 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“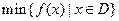 ”表示函数
”表示函数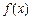 在集合D上的最小值,“
在集合D上的最小值,“ ”表示函数
”表示函数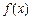 在集合D上的最大值.现设
在集合D上的最大值.现设 ,
,
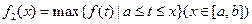 ,
,
若存在最小正整数k,使得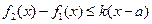 对任意的
对任意的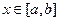 成立,则称函数
成立,则称函数
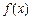 为区间
为区间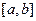 上的“第k类压缩函数”.
上的“第k类压缩函数”.
(Ⅰ) 若函数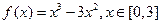 ,求
,求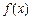 的最大值,写出
的最大值,写出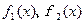 的解析式;
的解析式;
(Ⅱ) 若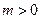 ,函数
,函数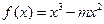 是
是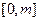 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围.
函数
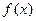 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“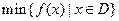 ”表示函数
”表示函数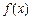 在集合D上的最小值,“
在集合D上的最小值,“ ”表示函数
”表示函数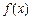 在集合D上的最大值.现设
在集合D上的最大值.现设 ,
,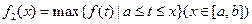 ,
,若存在最小正整数k,使得
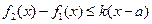 对任意的
对任意的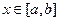 成立,则称函数
成立,则称函数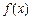 为区间
为区间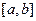 上的“第k类压缩函数”.
上的“第k类压缩函数”.
(Ⅰ) 若函数
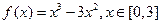 ,求
,求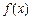 的最大值,写出
的最大值,写出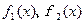 的解析式;
的解析式;(Ⅱ) 若
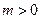 ,函数
,函数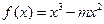 是
是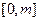 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围.解:(Ⅰ)由于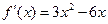 ,故
,故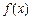 在
在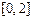 上单调递减,在
上单调递减,在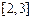 上单调递增.
上单调递增.
所以,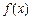 的最大值为
的最大值为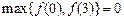 .………………3分
.………………3分
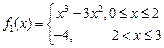 ,………………6分
,………………6分
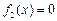 ,……………………………9分
,……………………………9分
(Ⅱ)由于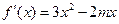 ,故
,故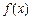 在
在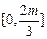 上单调递减,在
上单调递减,在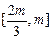 上单调递增,
上单调递增,
而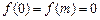 ,
,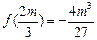 ,故
,故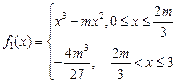 ,
,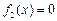 ,
,
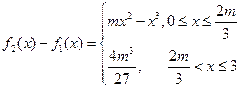 .……………………………11分
.……………………………11分
设对正整数k有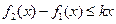 对
对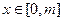 恒成立,
恒成立,
当x=0时,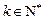 均成立;
均成立;
当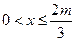 时,
时,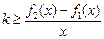 恒成立,
恒成立,
而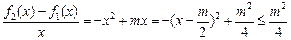 , 故
, 故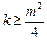 ;
;
当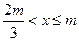 时,
时,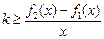 恒成立,而
恒成立,而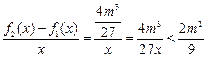 ;
;
故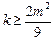 ;所以,
;所以,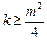 ,
,
又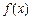
 是
是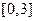 上的“第3类压缩函数”,故
上的“第3类压缩函数”,故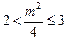 ,
,
所以,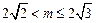 .…………14分
.…………14分
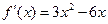 ,故
,故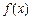 在
在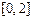 上单调递减,在
上单调递减,在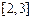 上单调递增.
上单调递增.所以,
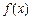 的最大值为
的最大值为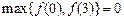 .………………3分
.………………3分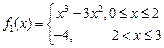 ,………………6分
,………………6分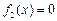 ,……………………………9分
,……………………………9分(Ⅱ)由于
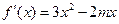 ,故
,故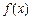 在
在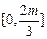 上单调递减,在
上单调递减,在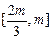 上单调递增,
上单调递增,而
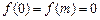 ,
,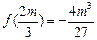 ,故
,故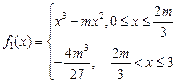 ,
,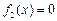 ,
,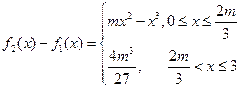 .……………………………11分
.……………………………11分设对正整数k有
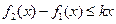 对
对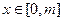 恒成立,
恒成立,当x=0时,
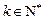 均成立;
均成立;当
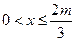 时,
时,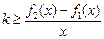 恒成立,
恒成立,而
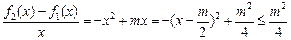 , 故
, 故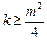 ;
;当
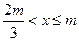 时,
时,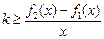 恒成立,而
恒成立,而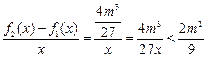 ;
;故
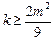 ;所以,
;所以,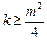 ,
,又
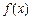
 是
是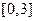 上的“第3类压缩函数”,故
上的“第3类压缩函数”,故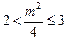 ,
,所以,
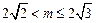 .…………14分
.…………14分略

练习册系列答案
相关题目
 的左、右焦点,点P在椭圆上运动,则
的左、右焦点,点P在椭圆上运动,则 的最大值是
的最大值是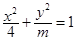 的离心率
的离心率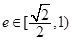 ,则
,则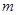 的取值范围为_____________.
的取值范围为_____________.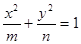 表示焦点在x轴上的椭圆有 个
表示焦点在x轴上的椭圆有 个 的对称轴为坐标轴,且抛物线
的对称轴为坐标轴,且抛物线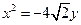 的焦点是椭圆
的焦点是椭圆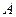
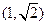 在椭圆
在椭圆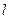 的方向向量为
的方向向量为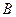 、
、 两点,求
两点,求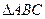 面积的最大值.
面积的最大值. 是椭圆
是椭圆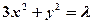 上的两点,点
上的两点,点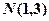 是线段
是线段 的中点,
的中点,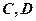 两点.
两点.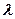 的取值范围,并求直线
的取值范围,并求直线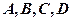 四点在同一个圆上?并说明理由.
四点在同一个圆上?并说明理由.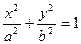
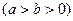 的一个顶点为
的一个顶点为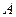
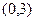 ,离心率
,离心率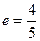
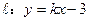 与椭圆交于不同的两点
与椭圆交于不同的两点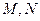 ,且满足
,且满足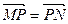 ,
,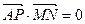 ,求直线
,求直线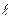 的方程.
的方程. 上一点,F1、F2为椭圆两焦点,若∠F1PF2=90°,则ΔF1PF2的面积等于( )
上一点,F1、F2为椭圆两焦点,若∠F1PF2=90°,则ΔF1PF2的面积等于( )
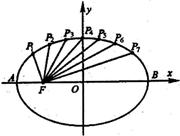
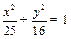 的长轴AB分成8等分,过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,…,P7七个点,F是椭圆的焦点,则|P1F|+|P2F|+…+|P7F|=" " .
的长轴AB分成8等分,过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,…,P7七个点,F是椭圆的焦点,则|P1F|+|P2F|+…+|P7F|=" " .