题目内容
已知f(x)=g(x)+2,且g(x)为奇函数,若f(2)=3,则f(-2)=
1
1
.分析:由已知可知f(2)=g(2)+2=3,可求g(2),然后把x=-2代入可得f(-2)=g(-2)+2=-g(2)+2可求f(-2)的值.
解答:解:∵f(x)=g(x)+2,f(2)=3,
∴f(2)=g(2)+2=3
∴g(2)=1
∵g(x)为奇函数
则f(-2)=g(-2)+2=-g(2)+2=1
故答案为:1.
∴f(2)=g(2)+2=3
∴g(2)=1
∵g(x)为奇函数
则f(-2)=g(-2)+2=-g(2)+2=1
故答案为:1.
点评:本题主要考查了利用函数的奇偶性求解函数的函数值,属于基础试题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
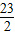 对任意n∈N*和任意实数x均成立,若存在求出满足条件的所有自然数M.
对任意n∈N*和任意实数x均成立,若存在求出满足条件的所有自然数M.