题目内容
曲线 与直线y=k(x-1)+2有两个交点时,实数k的取值范围是
与直线y=k(x-1)+2有两个交点时,实数k的取值范围是
- A.
 ≤k>1
≤k>1 - B.

- C.
 ≥K≥1
≥K≥1 - D.1≥k<

B
分析:数形结合来求,因为曲线y= 表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,y=k(x-1)+2是过定点(1,2)的直线,只要把该直线平行移动,看k为何时直线与曲线y=
表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,y=k(x-1)+2是过定点(1,2)的直线,只要把该直线平行移动,看k为何时直线与曲线y= 有两个交点即可.
有两个交点即可.
解答:∵y= 表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,
表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,
作出曲线y= 的图象,在同一坐标系中,再作出过定点(1,2)的直线,由左向右
的图象,在同一坐标系中,再作出过定点(1,2)的直线,由左向右
逆时针转动,
可发现,直线先与圆相切,切点为N(如图),直线l从AN开始逆时针转动,l与曲线有二个交点,到AM结束,
∵O到切线AN的距离d= =1,
=1,
∴k= ,
,
又直线AM的斜率为:kAM= =1,
=1,
∴实数k的取值范围是则 <k≤1.
<k≤1.
故选B.
点评:本题考查直线与圆的位置关系,着重考查了数形结合求直线与曲线交点个数的问题,属于中档题.
分析:数形结合来求,因为曲线y=
 表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,y=k(x-1)+2是过定点(1,2)的直线,只要把该直线平行移动,看k为何时直线与曲线y=
表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,y=k(x-1)+2是过定点(1,2)的直线,只要把该直线平行移动,看k为何时直线与曲线y= 有两个交点即可.
有两个交点即可.解答:∵y=
 表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,
表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,作出曲线y=
 的图象,在同一坐标系中,再作出过定点(1,2)的直线,由左向右
的图象,在同一坐标系中,再作出过定点(1,2)的直线,由左向右逆时针转动,

可发现,直线先与圆相切,切点为N(如图),直线l从AN开始逆时针转动,l与曲线有二个交点,到AM结束,
∵O到切线AN的距离d=
 =1,
=1,∴k=
 ,
,又直线AM的斜率为:kAM=
 =1,
=1,∴实数k的取值范围是则
 <k≤1.
<k≤1.故选B.
点评:本题考查直线与圆的位置关系,着重考查了数形结合求直线与曲线交点个数的问题,属于中档题.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
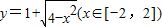 与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )
与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )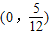
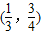
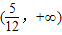
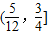
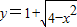 与直线y=k(x-2)+4有两个交点,则实数k的取值范围为 .
与直线y=k(x-2)+4有两个交点,则实数k的取值范围为 . 与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )
与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )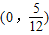
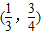
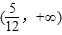
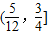
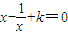 在x∈(0,1)没有实数根,则k的取值范围是k≥2
在x∈(0,1)没有实数根,则k的取值范围是k≥2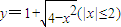 与直线y=k(x-2)+4有两个交点时,实数k的取值范围是
与直线y=k(x-2)+4有两个交点时,实数k的取值范围是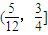
 的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是
的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是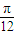 ,其中正确的结论是: .
,其中正确的结论是: . 与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )
与直线y=k(x-2)+4两个公共点时,实数k的取值范围是( )


