题目内容
 如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中A>0,ω>0,
如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中A>0,ω>0,| π |
| 2 |
y=f(x)=10sin(
x+
)+20,x∈[6,14]
| π |
| 8 |
| 3π |
| 4 |
y=f(x)=10sin(
x+
)+20,x∈[6,14]
.| π |
| 8 |
| 3π |
| 4 |
分析:由图中的最大值与最小值可求得b与A,由函数的周期可求得ω,由10ω+φ=2kπ,k∈Z,可求得φ.
解答:解:依题意,b=
=20,∵A>0,
∴30=A+b=A+20,
∴A=10;
又
=14-6=8,ω>0,
∴T=
=16,
∴ω=
,
∴y=f(x)=10sin(
x+φ)+20,
又f(10)=20,
∴
×10+φ=2kπ,(k∈Z),
∵
<φ<π,
∴φ=
.
∴y=f(x)=10sin(
x+
)+20,x∈[6,14].
故答案为:y=10sin(
x+
)+20,x∈[6,14].
| 30+10 |
| 2 |
∴30=A+b=A+20,
∴A=10;
又
| T |
| 2 |
∴T=
| 2π |
| ω |
∴ω=
| π |
| 8 |
∴y=f(x)=10sin(
| π |
| 8 |
又f(10)=20,
∴
| π |
| 8 |
∵
| π |
| 2 |
∴φ=
| 3π |
| 4 |
∴y=f(x)=10sin(
| π |
| 8 |
| 3π |
| 4 |
故答案为:y=10sin(
| π |
| 8 |
| 3π |
| 4 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得φ是难点,考查识图与应用的能力,属于中档题.

练习册系列答案
相关题目
 如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B(其中
如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B(其中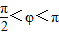 ),那么这一天6时至14时温差的最大值是 °C;与图中曲线对应的函数解析式是 .
),那么这一天6时至14时温差的最大值是 °C;与图中曲线对应的函数解析式是 .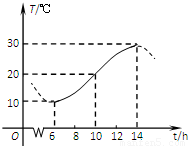
 ),那么与图中曲线对应的函数解析式是 .
),那么与图中曲线对应的函数解析式是 .
 (其中
(其中 ),
那么这一天6时至14时温差的最大值是________
),
那么这一天6时至14时温差的最大值是________ ;与图中曲线对应的函数解析式是______________
;与图中曲线对应的函数解析式是______________