题目内容

如图，圆O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F，且AB=2BP=4。
（1）求线段PF的长度；
（2）若圆F与圆O内切，直线PT与圆F切于点T，求线段PT的长度。
解：（1）连接OC，OD，OE，由同弧对应的圆周角与圆心角之间的关系结合题中条件弧长AE等于弧长AC可得∠CDE=∠AOC
又∠CDE=∠P+∠PFD，∠AOC=∠P+∠OCP，
从而∠PFD=∠OCP，
故△PFD∽△PCO，
由割线定理知PC·PD=PA·PB=12，
故。
（2）若圆F与圆O内切，设圆F的半径为r，
因为OF=2-r=1，即r=1，
所以OB是圆F的直径，且过P点圆F的切线为PT
则PT2=PB·PO=2×4=8，即。
练习册系列答案
相关题目
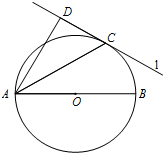精英家教网如图，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，过A作l的垂线AD，垂足为D，则线段CD的长为
 
．
精英家教网如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，则线段AE的长为
 
．
（2012•天门模拟）（1）如图，圆O的直径AB=8，C为圆周上一点，BC=4，过点C作圆的切线l，过点A作直线l的垂线AD，D为垂足，AD与圆O交于点E，则线段AE的长为
4
4
．
（2）在平面直角坐标系下，曲线C1：
x=2t+2a
y=-t
（t为参数），曲线C2：
x=2sinθ
y=1+2cosθ
（θ为参数），若曲线C1、C2有公共点，则实数a的取值范围为
[1-
5
，1+
5
]
[1-
5
，1+
5
]
．
（2013•盐城一模）[A．（选修4-1：几何证明选讲）
如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（几何证明选做题） 如图，圆O的直径AB=10，弦DE⊥AB于点H，HB=2．则DE=
8
8
．
B．（坐标系与参数方程选做题）已知直线C1
x=1+tcosα
y=tsinα
（t为参数），C2
x=cosθ
y=sinθ
（θ为参数），当α=
π
3
时，C1与C2的交点坐标为
(1，0)；(
1
2
，-
3
2
)
(1，0)；(
1
2
，-
3
2
)
．
C．（不等式选做题）若不等式|2a-1|≤|x+
1
x
|对一切非零实数a恒成立，则实数a的取值范围
[-
1
2
，
3
2
]
[-
1
2
，
3
2
]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网