Question

【题目】如图，在五棱锥中，平面平面，且．

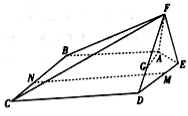
（1）已知点在线段上，确定的位置，使得平面；

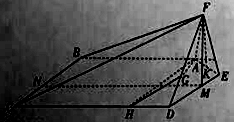
（2）点分别在线段上，若沿直线将四边形向上翻折，与恰好重合，求三棱锥的体积．

Answer 1

【答案】（1）为靠近的三等分点；（2）.

【解析】

试题分析：（1）本题的五棱锥的底面可视为正方形折起一个角,先由线线平行推得面面平行,从而得到线面平行；（2）先由面面垂直得到线面垂直和线线垂直,由翻折后重合,即求出的长度,所求的三棱锥体积,以三角形为底,为高,代入体积公式.

试题解析：解：（1）点为靠近的三等分点，

在线段取一点，使得，连结

∵，∴．

又，∴四边形为平行四边形，∴，

∵点为靠近的三等分点，∴，∴，

∵，∴平面平面，而平面，∴平面

（2）连接，根据条件可以求得，又，∴

取的中点，连接，∵，∴，又平面平面，

∴平面，∴

设，∵，∴

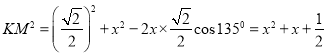
∵翻折后，与重合，∴．

∴，∴

∴