题目内容
设
0<x<1,a>0,且a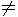 1,比较
1,比较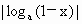 与
与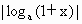 的大小.
的大小.
答案:略
解析:
解析:
|
解法一:当 a>1时,∵0<x<1则1+x>1,0<1-x<1,∴ 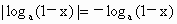 , ,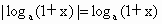 ,则有 ,则有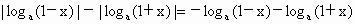 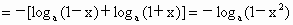 . .
∵ a>1,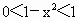 ∴ ∴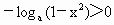 .∴ .∴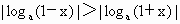 . .
当 0<a<1时,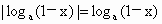 . .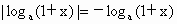 , ,
则有  . .
∵ 0<a<1,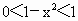 ,∴ ,∴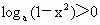 .∴ .∴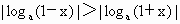 . .
因此,当 0<x<1,a>0,且a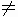 1时,总有 1时,总有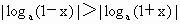 . .
解法二: 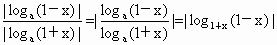 . .
∵ 1+x>1,0<1-x<1,∴ 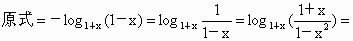
∵ 1+x>1,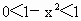 , ,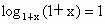 , ,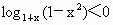 , ,
∴  . .
即 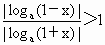 ,∴ ,∴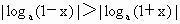 . .
(1) 此题的解答过程中有两个关键的步骤:一是比较两个实数大小的出发点和基本方法(作差比较法与作商比较法).二是利用对数函数的性质处理两个绝对值符号和进行对数式的变换与计算.(2) 比较以上解法各有优点,解法1中,分0<a<1和a>1两种情况进行讨论的思想方法是具有普通意义的;而解法2比解法1简便,其原因是充分注意到了所需要比较大小的是两个正数,同时巧妙地运用了换底公式,从而避开了对底数a的讨论.(3) 含绝对值的问题,一般要去掉绝对值研究,这是一个基本观点.去绝对值时,注意对谁取绝对值就对谁讨论.|f(x)|当f(x)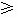 0时为f(x),当f(x)<0时为-f(x). 0时为f(x),当f(x)<0时为-f(x). |

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
设0<x<1,a、b为正常数,则
+
的最小值为( )
| a2 |
| x |
| b2 |
| 1-x |
| A、4ab |
| B、2(a2+b2) |
| C、(a+b)2 |
| D、(a-b)2 |
