Question

如图，在面积为18的△ABC中，AB=5，双曲线E过点A，

且以B、C为焦点，已知

（Ⅰ）建立适当的坐标系，求双曲线E的方程；

（Ⅱ）是否存在过点D（1，1）的直线l，

使l与双曲线E交于不同的两点M、N，且

如果存在，求出直线l的方程；如果不存在，请说明理由.

Answer 1

（Ⅰ）（Ⅱ）不存在满足条件的直线l.

解析:

（Ⅰ）以BC所在直线为x轴，线段BC的中点O为原点，线段BC的中垂线为y轴建立坐标系如图.  设  2分

    则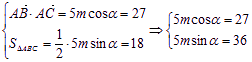  两式平方相加，得m=9.   ………2分

又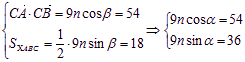两式平方相加，得   2分

设双曲线的方程为     由双曲线的定义，

有2a=||AC|－|AB||=|m－5|=4，即a=2.    又2c=，即

∴b²=c²－a²=9.     ∴双曲线E的方程为 ……2分

（Ⅱ）假设存在满足条件的直线l，使l与双曲线E交于不同两点M、N，

并设  由知点D是线段MN的中点，

∴  …………1分    由于点M、N都在双曲线E上，

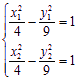∴.    将两式相减，得

此时直线l的方程为  ……3分

但由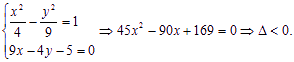∴不存在满足条件的直线l.  …2分