题目内容
已知向量a=
 ,b=
,b= ,c=
,c= ,
,
(1)求证:(a+b)⊥(a-b);
(2)设函数
 ,求
,求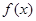 的最大值和最小值.[来
的最大值和最小值.[来
【答案】
(2)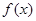 的最大值为4,最小值为0.
的最大值为4,最小值为0.
【解析】(1)计算向量的数量积;(2)将f(x)化为 4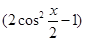 . 再由x∈
. 再由x∈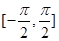 ,
得
,
得 ∈
∈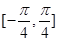 求解.
求解.
解:(1)【解法一】依题意得:a+b=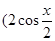 ,
,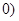 ,a-b=
,a-b=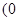 ,
,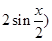
∴(a+b)·(a-b)=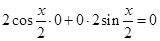 ,
,
∴(a+b)⊥(a-b). (5分)
【解法二】依题意得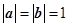 ,∴(a+b)·(a-b)=
,∴(a+b)·(a-b)=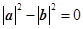 ,
,
∴(a+b)⊥(a-b). (5分)
(2)依题意得a+c=(cos +1,sin
+1,sin -1),b+c=(cos
-1),b+c=(cos +1,-sin
+1,-sin -1),
-1),
∴|a+c|2-3=(cos +1)2+(sin
+1)2+(sin -1)2-3=2cos
-1)2-3=2cos -2sin
-2sin ,
,
|b+c|2-3=(cos +1)2+(-sin
+1)2+(-sin -1)2-3=2cos
-1)2-3=2cos +2sin
+2sin ,
,
∴f(x)=(|a+c|2-3)(|b+c|2-3)=(2cos -2sin
-2sin )(2cos
)(2cos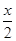 +2sin
+2sin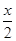 )
)
=4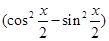 =4
=4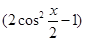 . 又x∈
. 又x∈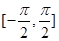 ,
∴
,
∴ ∈
∈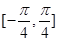
故当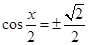 ,即
,即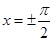 时,
时,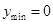 ;当
;当 ,即
,即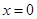 时,
时,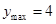
∴函数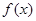 的最大值为4,最小值为0.
(12分)
的最大值为4,最小值为0.
(12分)

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ,b=(4,4cos α-
,b=(4,4cos α- ),若a⊥b,则sin
),若a⊥b,则sin 等于( )
等于( ) B.-
B.-