题目内容
【题目】已知椭圆方程 
为： 
椭圆的右焦点为 
，离心率为 
，直线 
与椭圆 相交于 
两点，且 
（1）椭圆的方程
（2）求 
的面积；
【答案】
（1）解：由已知 
，∴ 
，∴ 
椭圆方程为： 
（2）解：设 
， 
，则 
的坐标满足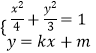 
消去 
化简得， 
， 
，得 
,
.
， 
，即 
∴ 
， 
到直线 
的距离 
∴ 
,
【解析】（1）由椭圆过一点及离心率两个条件列出关于a,b,c的方程组求a,b,c。
（2）将直线方程和椭圆方程联立成方程组，消去y得关于x的一元二次方程，由韦达定理及弦长公式得到k与m的关系，由弦长公式求弦长。
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
练习册系列答案
相关题目
