题目内容
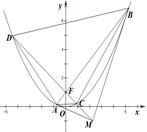
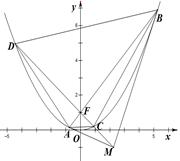
如图,已知抛物线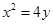 的焦点为
的焦点为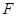 ,过焦点
,过焦点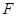 且不平行于
且不平行于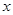 轴的动直线
轴的动直线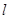 交抛物线于
交抛物线于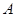 ,
,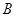 两点,抛物线在
两点,抛物线在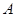 、
、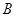 两点处的切线交于点
两点处的切线交于点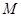 .
.
(Ⅰ)求证: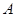 ,
,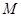 ,
,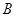 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(Ⅱ)设直线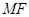 交该抛物线于
交该抛物线于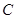 ,
,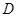 两点,求四边形
两点,求四边形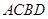 面积的最小值.
面积的最小值.
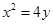 的焦点为
的焦点为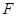 ,过焦点
,过焦点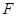 且不平行于
且不平行于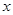 轴的动直线
轴的动直线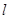 交抛物线于
交抛物线于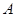 ,
,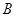 两点,抛物线在
两点,抛物线在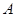 、
、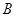 两点处的切线交于点
两点处的切线交于点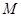 .
.
(Ⅰ)求证:
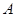 ,
,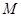 ,
,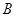 三点的横坐标成等差数列;
三点的横坐标成等差数列;(Ⅱ)设直线
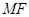 交该抛物线于
交该抛物线于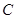 ,
,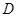 两点,求四边形
两点,求四边形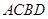 面积的最小值.
面积的最小值.(Ⅰ)可设直线 的方程
的方程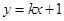 (
(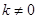 ),
),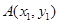 ,
,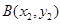 ,由
,由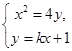 消去
消去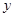 ,得
,得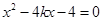 ,
,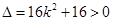 .
. 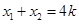 ,
,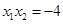 ,由
,由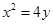 ,得
,得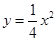 ,所以
,所以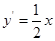 ,直线
,直线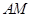 的斜率为
的斜率为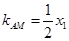 直线
直线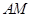 的方程为
的方程为 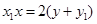 同理,直线
同理,直线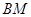 的方程为
的方程为  M的横坐标
M的横坐标 即
即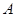 ,
,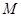 ,
,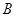 三点的横坐标成等差数列(Ⅱ)32
三点的横坐标成等差数列(Ⅱ)32
 的方程
的方程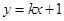 (
(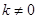 ),
),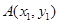 ,
,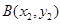 ,由
,由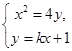 消去
消去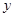 ,得
,得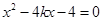 ,
,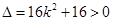 .
. 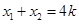 ,
,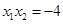 ,由
,由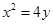 ,得
,得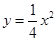 ,所以
,所以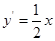 ,直线
,直线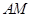 的斜率为
的斜率为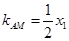 直线
直线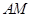 的方程为
的方程为 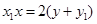 同理,直线
同理,直线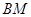 的方程为
的方程为  M的横坐标
M的横坐标 即
即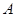 ,
,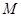 ,
,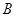 三点的横坐标成等差数列(Ⅱ)32
三点的横坐标成等差数列(Ⅱ)32试题分析:(Ⅰ)由已知,得
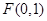 ,显然直线
,显然直线 的斜率存在且不为0,则可设直线
的斜率存在且不为0,则可设直线 的方程
的方程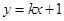 (
(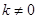 ),
),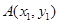 ,
,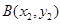 ,
, 
由
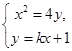 消去
消去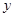 ,得
,得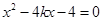 ,
,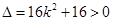 .
. 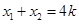 ,
,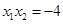 2分
2分由
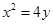 ,得
,得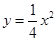 ,所以
,所以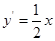 ,直线
,直线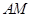 的斜率为
的斜率为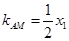 ,
,所以,直线
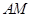 的方程为
的方程为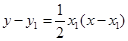 ,又
,又 ,
,所以,直线
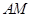 的方程为
的方程为 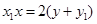 ① 4分
① 4分同理,直线
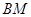 的方程为
的方程为  ② 5分
② 5分②-①并据
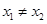 得点M的横坐标
得点M的横坐标 ,
,即
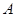 ,
,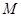 ,
,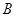 三点的横坐标成等差数列 7分
三点的横坐标成等差数列 7分(Ⅱ)由①②易得y=-1,所以点M的坐标为(2k,-1)(
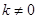 ).
).所以
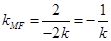 ,则直线MF的方程为
,则直线MF的方程为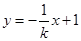 8分
8分设C(x3,y3),D(x4,y4), 由
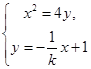 消去
消去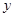 ,得
,得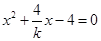 ,
,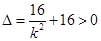
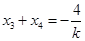 ,
,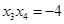 . 9分
. 9分又
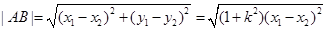
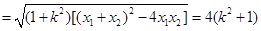 10分
10分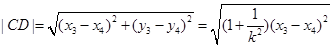
 12分
12分因为
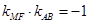 ,所以
,所以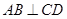 ,
,所以,
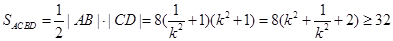 ,
,当且仅当
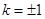 时,四边形
时,四边形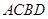 面积的取到最小值
面积的取到最小值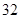 14分
14分点评:当直线与圆锥曲线相交时,常联立方程组转化为关于x的二次方程,进而利用方程的根与系数的关系设而不求的方法化简,在求解时弦长公式
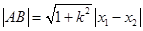 经常用到,本题中函数在某一点的切线问题要借助于导数的几何意义求出切线斜率
经常用到,本题中函数在某一点的切线问题要借助于导数的几何意义求出切线斜率
练习册系列答案
相关题目
 与曲线
与曲线 的交点个数为( )
的交点个数为( )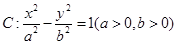 的离心率为
的离心率为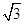 ,右准线方程为
,右准线方程为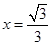 。
。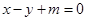 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆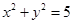 上,求实数m的值。
上,求实数m的值。 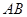 是平面
是平面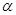 的斜线段,
的斜线段,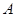 为斜足。若点
为斜足。若点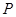 在平面
在平面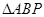 的面积为定值,则动点
的面积为定值,则动点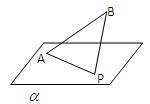
 是抛物线
是抛物线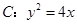 的焦点,
的焦点,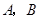 是
是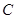 上的两个点,线段AB的中点为
上的两个点,线段AB的中点为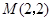 ,则
,则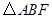 的面积等于
的面积等于  ,点
,点 位于该双曲线上,线段
位于该双曲线上,线段 的中点坐标为
的中点坐标为 ,则该双曲线的标准方程为
,则该双曲线的标准方程为



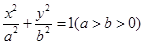 的左、右焦点分别为F1,F2,椭圆的离心率为
的左、右焦点分别为F1,F2,椭圆的离心率为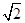 :2.(1)过点C(-1,0)且以向量
:2.(1)过点C(-1,0)且以向量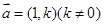 为方向向量的直线
为方向向量的直线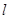 交椭圆于不同两点A、B,若
交椭圆于不同两点A、B,若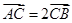 ,则当△OAB的面积最大时,求椭圆的方程。
,则当△OAB的面积最大时,求椭圆的方程。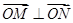 ,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.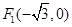 ,
,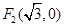 ,过
,过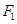 且与坐标轴不平行的直线
且与坐标轴不平行的直线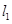 与椭圆交于
与椭圆交于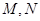 两点,如果
两点,如果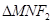 的周长等于8。
的周长等于8。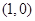 的直线
的直线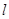 与椭圆交于不同两点
与椭圆交于不同两点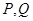 ,试问在
,试问在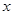 轴上是否存在定点
轴上是否存在定点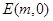 ,使
,使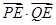 恒为定值?若存在,求出点
恒为定值?若存在,求出点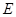 的坐标及定值;若不存在,说明理由。
的坐标及定值;若不存在,说明理由。 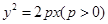 的焦点
的焦点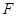 且斜率为
且斜率为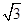 的直线与抛物线交于
的直线与抛物线交于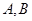 两点,且
两点,且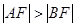 ,则
,则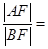 .
.