题目内容
在△ABC中，已知
·
?=9，sinB=cosAsinC,面积S△ABC=6.（1）求△ABC的三边的长；
（2）设P是△ABC（含边界）内一点，P到三边AC、BC、AB的距离分别为x、y和z，求x+y+z的取值范围.
解：设AB=c,AC=b,BC=a.
(1)tanA=
,sinA=
,cosA=
,bc=15.
=cosA
=
,由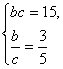
用余弦定理得a=4.
(2)2S△ABC=3x+4y+5z=12
x+y+z=
+
(2x+y),
设t=2x+y,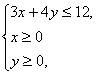
由线性规划得0≤t≤8.
∴
≤x+y+z≤4.
练习册系列答案
相关题目