题目内容
求解下列问题(1)求函数
 的定义域;
的定义域;(2)求f(x)=sin(
 )的单调增区间;
)的单调增区间;(3)函数f(x)=
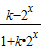 为奇函数,求k的值.
为奇函数,求k的值.
【答案】分析:(1)由偶次根式内部的代数式大于等于0,对数式的真数大于0,联立后求解三角不等式即可得到函数的定义域;
(2)给出的函数是正弦型的复合函数,且内层函数为减函数,只要让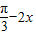 在正弦函数的减区间内求解x的取值范围即可,最后用区间表示;
在正弦函数的减区间内求解x的取值范围即可,最后用区间表示;
(3)根据函数是奇函数的定义,由f(-x)+f(x)=0恒成立,列式后得(k2-1)(22x+1)=0恒成立,也就是k2-1=0恒成立,则k的值可求.
解答:解:(1)要使原函数有意义,
则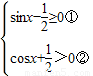 ,
,
解①得: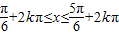 (k∈Z),
(k∈Z),
解②得: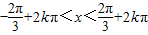 (k∈Z).
(k∈Z).
所以,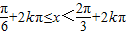 (k∈Z).
(k∈Z).
所以,原函数的定义域为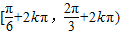 (k∈Z).
(k∈Z).
(2)令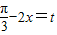 ,
,
则内层函数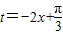 为减函数,
为减函数,
由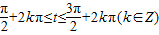 ,
,
即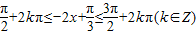 ,
,
解得: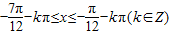 .
.
即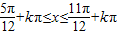 (k∈Z).
(k∈Z).
所以,函数f(x)=sin(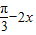 )的单调增区间为:
)的单调增区间为:
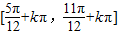 (k∈Z).
(k∈Z).
(3)由函数f(x)=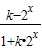 为奇函数,
为奇函数,
则f(-x)+f(x)=0恒成立,
即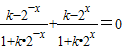 恒成立,
恒成立,
整理得: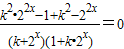 ,
,
所以,(k2-1)(22x+1)=0恒成立.
即k2-1=0恒成立.
所以,k=1 或k=-1.
所以,使函数f(x)=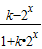 为奇函数的k的值为1或-1.
为奇函数的k的值为1或-1.
点评:本题考查了函数的定义域及其求法,考查了复合函数的单调性,考查了函数的奇偶性,复合函数的单调性满足“同增异减”的原则,运用函数奇偶性求解参数时,注意等式恒成立的条件,此题是中档题.
(2)给出的函数是正弦型的复合函数,且内层函数为减函数,只要让
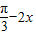 在正弦函数的减区间内求解x的取值范围即可,最后用区间表示;
在正弦函数的减区间内求解x的取值范围即可,最后用区间表示;(3)根据函数是奇函数的定义,由f(-x)+f(x)=0恒成立,列式后得(k2-1)(22x+1)=0恒成立,也就是k2-1=0恒成立,则k的值可求.
解答:解:(1)要使原函数有意义,
则
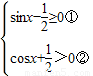 ,
,解①得:
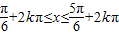 (k∈Z),
(k∈Z),解②得:
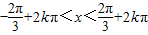 (k∈Z).
(k∈Z).所以,
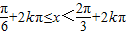 (k∈Z).
(k∈Z).所以,原函数的定义域为
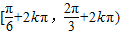 (k∈Z).
(k∈Z).(2)令
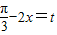 ,
,则内层函数
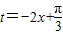 为减函数,
为减函数,由
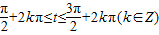 ,
,即
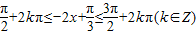 ,
,解得:
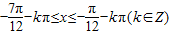 .
.即
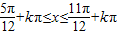 (k∈Z).
(k∈Z).所以,函数f(x)=sin(
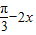 )的单调增区间为:
)的单调增区间为: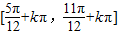 (k∈Z).
(k∈Z).(3)由函数f(x)=
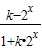 为奇函数,
为奇函数,则f(-x)+f(x)=0恒成立,
即
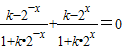 恒成立,
恒成立,整理得:
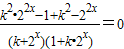 ,
,所以,(k2-1)(22x+1)=0恒成立.
即k2-1=0恒成立.
所以,k=1 或k=-1.
所以,使函数f(x)=
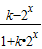 为奇函数的k的值为1或-1.
为奇函数的k的值为1或-1.点评:本题考查了函数的定义域及其求法,考查了复合函数的单调性,考查了函数的奇偶性,复合函数的单调性满足“同增异减”的原则,运用函数奇偶性求解参数时,注意等式恒成立的条件,此题是中档题.

练习册系列答案
相关题目
 中,
中, 分别是
分别是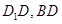 的中点,
的中点,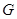 在棱
在棱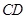 上,且
上,且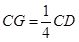 ,H为
,H为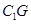 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.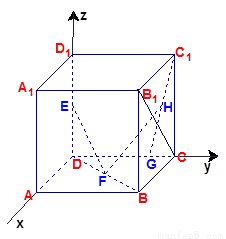
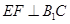 ;
; 的定义域;
的定义域;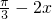 )的单调增区间;
)的单调增区间; 为奇函数,求k的值.
为奇函数,求k的值.