Question

椭圆E：

x2

a2

+y²=1（a＞1）与双曲线H：

x2

m2

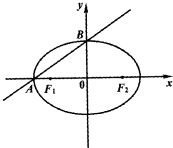
-y²=1（m＞0）有相同的焦点F₁，F₂，E与H在第一象限的交点为P，则△PF₁F₂的面积为（　　）

• A．

  1

  2

• B．1
• C．

  3

  2

• D．2

Answer 1

分析：利用椭圆、双曲线的定义，求出|PF₁|=m+a，|PF₂|=a-m，结合椭圆E：

x2

a2

+y²=1（a＞1）与双曲线H：

x2

m2

-y²=1（m＞0）有相同的焦点，可求得∠F₁PF₂=90°，从而可得△PF₁F₂的面积．

解答：解：由题意，|PF₁|-|PF₂|=2m，|PF₁|+|PF₂|=2a
∴|PF₁|=m+a，|PF₂|=a-m
∵椭圆E：

x2

a2

+y²=1（a＞1）与双曲线H：

x2

m2

-y²=1（m＞0）有相同的焦点
∴a²-1=m²+1
∴a²-m²=2
∴cos∠F₁PF₂=

2m2+2a2-4(a2-1)

2(m+a)(m-a)

=

2m2+2a2-4(a2-1)

2(m+a)(a-m)

=

0

2×2

=0
∴∠F₁PF₂=90°
∴△PF₁F₂的面积为

1

2

|PF₁||PF₂|=

1

2

（a²-m²）=1
故选B．

点评：本题考查椭圆、双曲线的定义，考查余弦定理的运用，考查三角形面积的计算，属于中档题．