题目内容
 如图,椭圆中心在坐标原点,F为左焦点,当
如图,椭圆中心在坐标原点,F为左焦点,当 时,其离心率为
时,其离心率为 ,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为
,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为
- A.

- B.

- C.
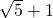
- D.
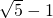
A
分析:类比“黄金椭圆”,在黄金双曲线中,当 时,|BF|2+|AB|2=|AF|2,由此可知b2+c2+c2=a2+c2+2ac,整理得c2=a2+ac,即e2-e-1=0,解这个方程就能求出黄金双曲线的离心率e.
时,|BF|2+|AB|2=|AF|2,由此可知b2+c2+c2=a2+c2+2ac,整理得c2=a2+ac,即e2-e-1=0,解这个方程就能求出黄金双曲线的离心率e.
解答:类比“黄金椭圆”,在黄金双曲线中,|OA|=a,|OB|=b,|OF|=c,
当 时,|BF|2+|AB|2=|AF|2,
时,|BF|2+|AB|2=|AF|2,
∴b2+c2+c2=a2+c2+2ac,
∵b2=c2-a2,整理得c2=a2+ac,
∴e2-e-1=0,解得 ,或
,或  (舍去).
(舍去).
故黄金双曲线的离心率 .
.
故选A.
点评:本题主要考查了类比推理、椭圆的简单性质及双曲线的简单性质.注意寻找黄金双曲线中a,b,c之间的关系,利用双曲线的性质求解.
分析:类比“黄金椭圆”,在黄金双曲线中,当
 时,|BF|2+|AB|2=|AF|2,由此可知b2+c2+c2=a2+c2+2ac,整理得c2=a2+ac,即e2-e-1=0,解这个方程就能求出黄金双曲线的离心率e.
时,|BF|2+|AB|2=|AF|2,由此可知b2+c2+c2=a2+c2+2ac,整理得c2=a2+ac,即e2-e-1=0,解这个方程就能求出黄金双曲线的离心率e.解答:类比“黄金椭圆”,在黄金双曲线中,|OA|=a,|OB|=b,|OF|=c,
当
 时,|BF|2+|AB|2=|AF|2,
时,|BF|2+|AB|2=|AF|2,∴b2+c2+c2=a2+c2+2ac,
∵b2=c2-a2,整理得c2=a2+ac,
∴e2-e-1=0,解得
 ,或
,或  (舍去).
(舍去).故黄金双曲线的离心率
 .
.故选A.
点评:本题主要考查了类比推理、椭圆的简单性质及双曲线的简单性质.注意寻找黄金双曲线中a,b,c之间的关系,利用双曲线的性质求解.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 如图,椭圆中心在坐标原点,F为左焦点,当
如图,椭圆中心在坐标原点,F为左焦点,当 如图,椭圆中心在坐标原点,焦点在坐标轴上,A、B是顶点,F是左焦点;当BF⊥AB时,此类椭圆称为“黄金椭圆”,其离心率为
如图,椭圆中心在坐标原点,焦点在坐标轴上,A、B是顶点,F是左焦点;当BF⊥AB时,此类椭圆称为“黄金椭圆”,其离心率为 如图,椭圆中心在坐标原点,点F为左焦点,点B为短轴的上顶点,点A为长轴的右顶点.当
如图,椭圆中心在坐标原点,点F为左焦点,点B为短轴的上顶点,点A为长轴的右顶点.当 如图,椭圆中心在坐标原点,F为左焦点,当
如图,椭圆中心在坐标原点,F为左焦点,当