题目内容
已知f(x)为定义在(-∞,0)∪(0,+∞)上的奇函数,x>0时,f(x)=1- ,
,
(1)求函数f(x)的解析式,
(2)判断函数f(x)在(0,+∞)的单调性并用定义证明.
解:(1)设x<0,则-x>0,f(-x)=1+ ,又∵f(x)为奇函数,
,又∵f(x)为奇函数,
∴f(x)=-f(x)=-1-
∴f(x)=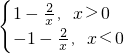
(2)f(x)在(0,+∞)为单调增函数.
证明:任取0<x1<x2,则f(x1)-f(x2)=1- -1+
-1+ =
= -
- =
=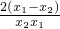
∵0<x1<x2,∴x1-x2<0,x1x2>0,
∴f(x1)-f(x2)<0,
∴f(x)在(0,+∞)为单调增函数.
分析:(1)只需求x<0时函数f(x)的解析式即可,利用奇函数的定义和已知x>0时,f(x)的解析式即可求得分段函数f(x)在定义域上的解析式;
(2)利用函数单调性的定义,任取0<x1<x2,利用作差法,证明f(x1)-f(x2)<0,即可证明函数f(x)在(0,+∞)的单调性
点评:本题主要考查了利用函数的奇偶性求函数解析式的方法,利用函数单调性的定义证明函数的单调性的方法,简单复合函数单调性的判断,代数变形和逻辑推理能力
 ,又∵f(x)为奇函数,
,又∵f(x)为奇函数,∴f(x)=-f(x)=-1-

∴f(x)=
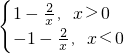
(2)f(x)在(0,+∞)为单调增函数.
证明:任取0<x1<x2,则f(x1)-f(x2)=1-
 -1+
-1+ =
= -
- =
=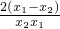
∵0<x1<x2,∴x1-x2<0,x1x2>0,
∴f(x1)-f(x2)<0,
∴f(x)在(0,+∞)为单调增函数.
分析:(1)只需求x<0时函数f(x)的解析式即可,利用奇函数的定义和已知x>0时,f(x)的解析式即可求得分段函数f(x)在定义域上的解析式;
(2)利用函数单调性的定义,任取0<x1<x2,利用作差法,证明f(x1)-f(x2)<0,即可证明函数f(x)在(0,+∞)的单调性
点评:本题主要考查了利用函数的奇偶性求函数解析式的方法,利用函数单调性的定义证明函数的单调性的方法,简单复合函数单调性的判断,代数变形和逻辑推理能力

练习册系列答案
相关题目
已知f(x)为定义在(-∞,+∞)上的可导函数,且f(x)<f′(x)对于x∈R恒成立,则( )
| A、f(2)>e2f(0),f(2010)>e2010f(0) | B、f(2)<e2f(0),f(2010)>e2010f(0) | C、f(2)>e2f(0),f(2010)<e2010f(0) | D、f(2)<e2f(0),f(2010)<e2010f(0) |
已知f(x)为定义在R上的奇函数,当x≥0时,f(x)=x(1+x),则当x<0时,有( )
| A、f(x)=-x(1+x) | B、f(x)=-x(1-x) | C、f(x)=x(1-x) | D、f(x)=x(x-1) |