题目内容
已知F1、F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则P到x轴的距离为( )
(A)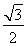 (B)
(B)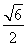 (C)
(C)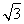 (D)
(D)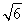
【答案】
B
【解析】由双曲线方程可知,a=1,b=1,c=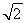 ,|F1F2|=2
,|F1F2|=2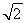 .
.
由双曲线定义有||PF1|-|PF2||=2a=2,①
在△F1PF2中,由余弦定理有:
8=|PF1|2+|PF2|2-2|PF1||PF2|cos60°②
联立①②解得|PF1||PF2|=4,设点P(x,y),
则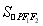 =
=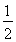 |PF1||PF2|sin60°=
|PF1||PF2|sin60°=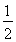 |F1F2||y|,
|F1F2||y|,
解得|y|=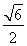 .故选B.
.故选B.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )