题目内容
证明对数换底公式: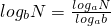 (a,b,N都是正数,a≠1,b≠1).
(a,b,N都是正数,a≠1,b≠1).
证明:令logbN=x,则bx=N,两边同取以a为底的对数得: =logaN,
=logaN,
∴x•logab=logaN,
∴x= ,
,
∴logbN= 成立.
成立.
分析:利用指数式与对数式的互化,logbN=x 等价于bx=N,两边同取对数后解除x的解析式.
点评:本题考查对数的定义,体现解方程的思想.
 =logaN,
=logaN,∴x•logab=logaN,
∴x=
 ,
,∴logbN=
 成立.
成立.分析:利用指数式与对数式的互化,logbN=x 等价于bx=N,两边同取对数后解除x的解析式.
点评:本题考查对数的定义,体现解方程的思想.

练习册系列答案
相关题目
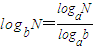 (a,b,N都是正数,a≠1,b≠1).
(a,b,N都是正数,a≠1,b≠1).