题目内容
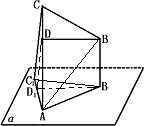
已知边长为2的正△ABC在平面α内,PA⊥α,PA=1,则点P到直线BC的距离为
2
2
.分析:画出图形,取BC的中点D,连接PD,AD,说明PD为所求,结合直角三角形,求解即可.
解答: 解:由题意画出图形,如图,取BC的中点D,连接PD,AD,
解:由题意画出图形,如图,取BC的中点D,连接PD,AD,
因为PA⊥α,△ABC是正三角形,AD⊥BC,PD⊥BC,PA∩AD=A,
所以BC⊥平面PAD,PD?平面PAD,所以BC⊥PD.
边长为2的正△ABC,AD=
=
,PA=1,
∵PA⊥α,∴PA⊥AD,
PD=
=
=2.
点P到直线BC的距离为PD=2.
故答案为:2.
 解:由题意画出图形,如图,取BC的中点D,连接PD,AD,
解:由题意画出图形,如图,取BC的中点D,连接PD,AD,因为PA⊥α,△ABC是正三角形,AD⊥BC,PD⊥BC,PA∩AD=A,
所以BC⊥平面PAD,PD?平面PAD,所以BC⊥PD.
边长为2的正△ABC,AD=
| 22-1 |
| 3 |
∵PA⊥α,∴PA⊥AD,
PD=
| PA2+AD2 |
12+(
|
点P到直线BC的距离为PD=2.
故答案为:2.
点评:本题是基础题,考查点到直线的距离的求法,正确找出点P到直线BC的距离是解题的关键,考查计算能力.

练习册系列答案
相关题目
已知P是边长为2的正△ABC的边BC上的动点,则
•(
+
)( )
| AP |
| AB |
| AC |
| A、最大值为8 | B、是定值6 |
| C、最小值为2 | D、是定值2 |
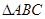 边BC上的动点,则
边BC上的动点,则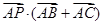 ( )
( )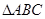 的边BC上的动点,则
的边BC上的动点,则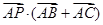 ( )
( )