Question

写出下面命题的逆命题、否命题与逆否命题，并分别指出四种命题的真假：

当2m+1＞0时，如果＞0,

那么m²－5m+6＜0.?

Answer 1

解：由2m+1＞0,得m＞－;?

由＞0,得m＜－3或m＞.?

又m＞－,得m＞.?

由m²－5m+6＜0,得2＜m＜3;?

由m＞－,得2＜m＜3.?

由此可知，原命题可变为“如果m＞,那么2＜m＜3.”显然是假命题.?

逆命题为“当2m+1＞0时，

如果m²－5m+6＜0，那么＞0.”

此命题即是“如果2＜m＜3，那么m＞”，是真命题.

否命题为“当2m+1＞0时，

如果≤0，

那么m²－5m+6≥0.”

因为?－＜m＜,?

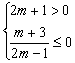
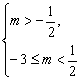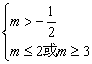
－＜m≤2或m≥3,?

则否命题可表述为“如果－＜m＜,那么－＜m≤2或m≥3”,是真命题.?

逆否命题为“当2m+1＞0时，

如果m²－5m+6≥0，那么≤0.”

它可表述为“如果－＜m≤2或m≥3,

那么－＜m＜”，是假命题.

点评：从集合的角度判断命题的真假有：“设AB,若x∈A则x∈B”是真命题，“设AB，若x∈A则x∈B”是假命题.